I’ve got a double-bill MathsJam recap for you this time, because I’ve been doing so much other stuff that I didn’t get round to writing up January’s MathsJam before the February one happened. I feel like I’ve forgotten most of what happened, so I’m working off my very brief notes.

January

My art teacher from school appeared in my office at uni one day saying he had a maths problem. He didn’t know I work here, so it was a shock to us both! His problem was:

Can you draw the same asymmetrical figure on all six faces of a cube, so that there’s no symmetry around any edge or vertex?

(He didn’t use exactly those words) Here’s what I mean, in pictures:

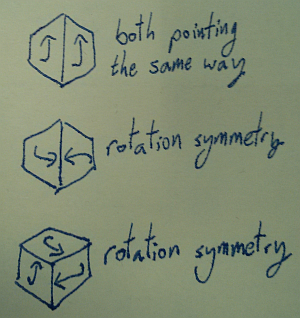
So on adjacent faces you can’t have the figure the same way up, or pointing in opposite directions, and you can’t have rotational symmetry around a vertex.

The answer to the question is no, but my proof is just an exhaustion of cases. It’s fun to work out, anyway. Thanks to the MathsJam Rubik’s cube and some arrows drawn on post-it notes, I think everyone eventually agreed it’s impossible, though there were some complaints that I kept “adding rules” whenever someone thought they’d come up with a counterexample.

Then we discussed a problem posted by Tanya Khovanova on her blog as an example of a coffin problem from the Moscow State University entrance exams:

Given four points on a square, reconstruct the square with straightedge and compass.

I can’t remember if we got the solution. It’s possible John showed us the solution he’d been shown, but I’m not sure.

John then showed us a little gizmo he’d made.

It has a number display and a button. The display starts at 1000, and every time you press the button it changes to a random lower number, until it gets to 1. You might want to watch this video I recorded of it in action. John asked us,

What’s the probability that it shows the number 2 before it gets to 1?

We all played with it for a bit (it’s quite compulsive), until after a while I realised I’d answered this problem before. The gizmo is doing the same thing as the seating passengers on a plane puzzle we solved last April. Top memory, CP! I also have written down that we considered the probability that every number is prime (or has some property X), but we must have just thought it up at the end.

Someone told us about this trick a lecturer had performed during a probability class, or something like that:

He asked everyone if they fancy the person sat next to them. It would be cruel to ask people to reveal that information in public, so he got everyone to flip two coins, and tell the truth only if they got two heads. How did he work out how many people fancy the person next to them?

I told everyone about David’s first sequence in the OEIS, sequence A189055: the primes which are the difference of consecutive eleventh powers. David had the idea, but I wrote a Sage notebook to compute the sequence. The notebook is mainly incomprehensible to me; we did some more investigating after finding the sequence but I’ve forgotten what.

I’ve written the question, “N points: how many topologies on them?” but I have absolutely no recollection of what that means.

Finally, I told everyone about my interesting times madness. I’m still suffering from it and it’s proven contagious, so I’ll spare you.

February

We started with a tricky puzzle I’d seen tweeted earlier in the day:

https://twitter.com/christianp/status/303791680480489472

Then I mentioned, for who knows what reason, Tarski’s high school algebra problem: there exist identities using only addition, multiplication and exponentiation on the positive integers that can’t be proved using the algebraic rules a typical high-school student is taught.

Eamonn showed us his odd Rubik’s cube. It’s one of these:

Stephen scrambled it and set to solving it, assuming Eamonn could put it right if he got stuck. Eamonn couldn’t, but fortunately it turned out that Stephen could.

John posed us a problem:

I have an infinite line of coins, all facing heads-up. I give you a template consisting of a finite number of arrows, which you can move along the line any number of times, flipping every coin pointed to by an arrow. Is it possible, no matter what the template is, to end up with exactly two coins facing tails-up?

Here’s an example of a template:

The proof involves the bane of my existence, generating functions. Yuck.

We discussed the coffin problems yet again. Possibly someone posed one of them not knowing where it came from. Then, there was some discussion of infinities. I wish I’d written more down!

I can very clearly remember doing some origami, but I have no written or photographic record of it. Instead, here’s one I made earlier:

It’s an icosahedron inside its dual, a dodecahedron.

For our last puzzle, I asked this unexpectedly easy question:

How many anagrams of the number $123456789$ are prime?

Finally, we talked about written versus spoken maths, after I’d discussed it on the All Squared podcast with Katie Steckles and Edmund Harriss.

Phew! I’m sure I’ve missed loads, but I’m glad I’ve finally written something down for the last two MathsJams.