Newcastle MathsJam March and April 2013 Recap
Here’s another double-bill MathsJam recap; I’ve been truly awful at keeping up this year.
The first thing I have written down in my notebook for March’s Newcastle MathsJam is a scribbled-upon sketch of what looks like some paths on a torus. I think I might’ve been explaining the definition of the fundamental group of a surface to someone.
Stephen brought in a whole collection of exotic Rubikish shapes. David decided to do art with them.
John brought The Mathematical Coloring Book:

Looking for
Not sure if this was posted on Twitter or brought up by someone at Newcastle. Here’s a solution:
- Let
- Then
- i.e.
- Quod erat to show.
Underneath that, I have couple of interesting identities:
That was tweeted by Jim Wilder, and is related to a very short integer sequence.
We must’ve been talking about nice number facts in general at this point, because I’ve written down my favourite number,
Numbers like this are called Münchausen numbers and belong to an exactly as tiny sequence as the factorions mentioned above. The paper “On a curious property of 3435” by Daan van Berkel will tell you all about them.
Eggs!
Easter happened in March, so Manchester MathsJam’s Katie and I researched ways of drawing mathematically-correct eggs beforehand. It doesn’t look like I kept any of our drawings, so you’ll just have to reconstruct them yourselves. All the literature we found on the subject (eggsegesis, if you will, and I hope you do) came from Germany. Jürgen Köller’s page on egg curves is comprehensive, while Herbert Möller’s paper, “Das 2:3-Ei – ein praktikables Eimodell“, gives a more rigorous treatment.
Inspired by our eggs, John reminded us of this problem that Ji had posed previously:
Given a circle and one point on it, draw an inscribed square with just a compass.
Difficult! I didn’t write down the answer!
I talked a bit about my friend Stacey’s problems with maximal oriented Wicks forms. Stacey copied out part of a proof she was studying on our office blackboard, and it was so attractive I took a picture and sent it in to the What’s on my blackboard? blog.
Next in my notebook is the word “Sarahdohedron”. Sarah made an unusual origami shape and needed a name for it.
We had a go at the jumping frogs puzzle, which the nice people at NRICH have recently made a nice version of. The lengths of solutions to the jumping frogs puzzle form yet another integer sequence, A005563.
We sort of had a conversation with Cardiff MathsJam through our respective Enigma machines. They were using a Pringles paper tube Enigma machine, but we cheated and used the Android app.
Night-night, Simon!
David presented us with a tricky problem of the utmost importance:
Simon the snake is very sleepy. He might fall asleep at any moment, in any position. What’s the smallest blanket can we use to be sure that we’ll entirely cover him, no matter what position he falls asleep in?
There was quite a lot of discussion about this. We started with a semicircle, which David reckoned you could cut a smaller arc out of the top of. I had some crazy cockahoop scheme involving variational methods that I won’t try to remember. Later on, we found out that Simon is the latest in a long line of sleepy slitherers which began with Moser’s worm. The paper “A smaller sleeping bag for a baby snake” by Svante Linusson, and Johan Wästlund has both a charming title and a much better solution than any of us came up with.
Recorded for posterity, here are our efforts:

Simon, pictured here on the edge of Sleepy Towne

Oh no, Simon has fallen asleep! Fetch the blanket!

Simon is moderately, but not optimally, snug underneath this blanket.

Sweet dreams, Simon. Sorry we weren’t clever enough to tuck you in to your exacting requirements.
Simon got a bit frayed towards the end of the night, so John offered to take him home and give him a bit of TLC. He reappeared in April with a neat heat-shrunk head. I assumed custody after that but I’m ashamed to say I have no idea where he is now. Hopefully, he’s having a little kip in the bottom of my backpack. I am a terrible snake-stepfather.
The last note I have is, “Is 10% the same thing as 0.1?”, prompted I think by an argument I was having with someone on Twitter. I’ll say that we agreed it is, because that way I win the argument.
Oh no, it’s the PAPAC-00
I’d hoped the main feature of April’s MathsJam would be the PAPAC-00, a cardboard computer I had assembled based on instructions I found on the internet. It didn’t really work though, so I just had to point to the bits that should’ve been moving when I pulled the control lever. Cereal box is not a precision medium. John said he thought it would work if the bits were made on a laser cutter. I expect to be surprised at May’s meeting.
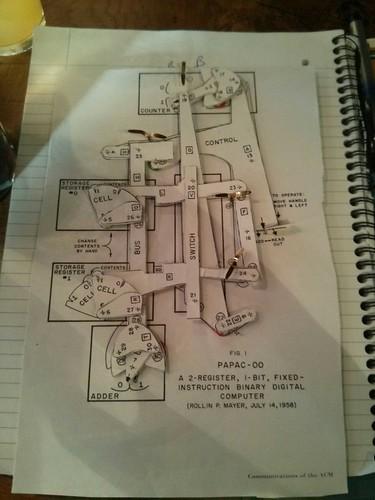
The Papac-00, in its natural state as a dream too beautiful for this mediocre reality.
The idea is that you set each of the two registers to store either 1 or 0, and then waggle the control lever back and forth. Each waggle of the lever adds the current register to the adder at the bottom. The counter at the top dictates which register is read, and alternates with each waggle. Roughly 13% of those things happened when I tried it.
We talked a bit about colourblindness, because I had just found the most marvellous app for my phone, which both simulates and corrects for colourblind vision through the phone’s camera. Everyone else learned how rubbish my view of the world is, and I learned a lot about what colours things are.
I had brought along the Big, Big, Big Book of Brainteasers, a book which made its first appearance at the third Newcastle MathsJam back in 2011. We tried a few puzzles – I’ve written down numbers 201 and 202 – before deciding they were either too easy, too hard, or too ambiguous to bother with. Eamonn had brought Erwin Brecher’s Puzzles, Brainteasers & Mathematical Diversions, which seemed to be a much better book. I’ve written down number 174, which I think might be a puzzle from Brechner’s book that we enjoyed. Any idea what it was, anyone?
Oh no, more circle construction problems
Here’s one:
A circle is inscribed in a quadrilateral. The ratio of the quadrilateral’s perimeter to the circle’s circumference is 3:2. What’s the ratio of the quadrilateral’s area to the circle’s?
And another:
Given a circle and a point outside it, construct the point’s tangents using only a ruler.
The solution to that one is so hard to find that I commented that many of these puzzles seem to arise when someone chances upon an interesting fact, then phrases it as a question. Asking peopel to do the inverse of that isn’t much fun, in my opinion. (#soreloser, I know)
The run-away train that failed to run away
Well-known interesting fact:
Little-known fascinating fact: the same sum but excluding numbers containing a 9 does converge!
In fact, you can pick any string of digits instead of “9”, even a really long one, and the fact is still true. It’s explained in the paper “Summing curious, slowly convergent, harmonic subseries” by Thomas Schmelzer and Robert Baillie.
Finally in my notebook, just this little bit:
. Others?
To be precise: we want two numbers such that, when you add their squares, you get their concatenation. Turns out Stephen’s done a lot of work on this since it was posed to him as part of an undergrad course (or problem sheet or something). He’s calculated an enormous number of solutions and put them on his website. He explained his method to us – maybe that’ll appear online too one day.
That’s a snapshot of two months’ worth of Newcastle MathsJams. I’ve missed quite a bit because I didn’t take very good notes, as usual. You’ll have noticed that we’re getting a bit hardcore again, without the influence of many non-academic mathmos. Since I get more than my fill of crazy super maths as a result of having to spend every working day with Cushing, and soon also Ji, I’m very keen to do some stress-free fun maths. So if you have any ideas how we can encourage more varied kinds of people to come to MathsJam, please tell me!
The next Newcastle MathsJam will be on Tuesday the 21st of May. If you’re one of the many people from outside Newcastle who read this blog, the MathsJam website lists over 30 cities round the world where MathsJams take place.



Comments
Comments
Alex Best
Maybe I’m missing something, but the harmonic series diverges right?
Nice roundup, I really want to try and make it to mathsjam at some point.
Joshua Zucker
Are there any other (interesting? nontrivial?) solutions to the
Also I think in your bit on the harmonic series at the end you said “converge” when you meant “diverge”.
Thanks for the fun collections of problems!
Christian Perfect
Yikes, it does! Consider the original version of this post the Bizarro Land version.
John
Credits time: The Mathematical Colouring Book was mine. Lots of lovely Ramsey theory. The squared circle problem was actually from Ji a few months earlier, but he was so quiet I was the only one who heard it. It’s such a lovely problem I had to re-introduce it once I knew the answer. And you were explaining the fundamental group of a surface to me.
a! = b!c! came about after seeing a post-card from the big MathsJam with 10! = 6!7! on it. That’s the only solution I’m aware of that isn’t a member of that family. Are there any others?
My favourite bit about the not-harmonic series is that the sum tends to 10^n log 10, where n is the length of the omitted string. It doesn’t matter what the string is. The electronic engineer in me was pleased to see a state machine in the proof of convergence.
Christian Perfect
Thanks for the corrections. I can always rely on you to remember things properly!
I also like the finite state machines in the harmonic subseries proof.
Michael Gibson
Just a quick (and possibly stupid) question..
Re: Given a circle and one point on it, draw an inscribed square with just a compass.
Just a compas, or a compas and straight edge? If is is the latter it seems fairly easy, but if it is the former then it seems impossible unless I’m missing something. How can you draw the straight edges of the square with a compas?? Unless we are just required to mark the positions of the vertices?
Christian Perfect
Just a compass, but just the corner points. It is possible!
Michael Gibson
Had to do a little bit of internet research for this one. Apprarently it is possible to do anything with just a compass that can be done with a compass and straight edge…
http://www.cut-the-knot.org/do_you_know/compass.shtml