primes = Primes()
def diff_pow(i,n):
return (i+1)**n - i**n
def diff_pow_primes(n,limit=range(1000)):
pows = [diff_pow(i,n) for i in limit]
return [p for p in pows if p in primes]
|
|
diff_pow_primes(11,range(1000))
[313968931, 6612607849, 68618940391, 2257404775627, 26360313735014491, 130898631716248441, 11736367906285382977, 28945284114821573731, 229761141540921525811, 202978059247932180748537, 228398127589553102936371, 476213535986962784582617, 1627839264198988265272849, 3421374091098795513254497, 9487926333956349725293849, 27709594721578130859474901, 48730115657671589642570917, 80484974300150990178920587, 133876864844857410396295099, 210933109270127551917779599, 258999347572773625770835081, 325834454057305251885058849, 718371836904538116928440187, 930509849625714272900586217, 1083363806077564819649665099, 1167960196969091338568804401, 1289994617266903346872449421, 5724743589263692562103249331, 6231603068728457682678816247, 9235528392739528351935195349, 40174841915931027745849420771, 43082207666387751794921615551, 46982047300312213527308215621, 56701738567387423020153786991, 63793487223197822181003010099, 211238111471708354115003215647, 234248866158658195723177119481, 295533862535252056957583609257, 516562885490814340488258665377, 750188442632294020948215731461, 996282696541122750795236458027, 1264883836069315290599058017731, 1656056265076012784944206936349, 3449323894408754669323484560291, 4549651325680387246801345529941, 6414852659086041896667159951349] |
for i in range(100):
if diff_pow(i,59) in primes:
print(i,diff_pow(i,11))
break
(2, 175099) |
def first_diff_pow_prime(n,limit=100):
i=1
for i in range(limit):
p=diff_pow(i,n)
if p in primes:
return p
|
|
firsts = [(i,first_diff_pow_prime(i,1000)) for i in range(3,130,2)]
firsts = [(n,f) for n,f in firsts if f]
|
|
#this is sequence A121620
for n,f in firsts:
print('%i: %i' % (n,f))
3: 7 5: 31 7: 127 11: 313968931 13: 8191 17: 131071 19: 524287 23: 777809294098524691 29: 68629840493971 31: 2147483647 37: 114867606414015793728780533209145917205659365404867510184121 41: 44487435359130133495783012898708551 43: 1136791005963704961126617632861 47: 22137406298265966315641393147750228275603823278911109 53: 19383245658672820642055731 59: 14130386091162273752461387579 61: 2305843009213693951 67: 418364165757172442919546303805118823151668308251259902807 71: 13085128045303706475631702887291899593573186840450238244455475662193\ 0025436662224870381199 73: 91588019915633166327821690138276466521280222166861730175848250090666\ 510342315068733846348990364669227925344611954091714991 79: 22085009220935559199979332104056352638217821922055936803895131909665\ 6329 83: 38597010273382026865943479201909913542774057395694590257401367491 89: 618970019642690137449562111 97: 17483671956120726428776222029037967515617870133177694509069678146342\ 78510769014706345922411228093685770776776526899400455455452849492405\ 51 101: 1546132562196033990574082188840405015112916155251 103: 14347469270160773061146152935978912255600824839787243434942098942438\ 56576751068883816801360961988642120733691856993378000902575332059446\ 60613596313746521662909586240167 107: 162259276829213363391578010288127 109: 26287834404118229883274579371659572846597956081404399348392468051632\ 282855938300124799455596540285764687297371474275953021 113: 11198720577036739030485084520362285149605831355174134378660530789611\ 63653331772846595095499688594127481 127: 170141183460469231731687303715884105727 |
from math import log10,log
for n,f in firsts:
print('%i: %0.20f' % (n,log(f)/n))
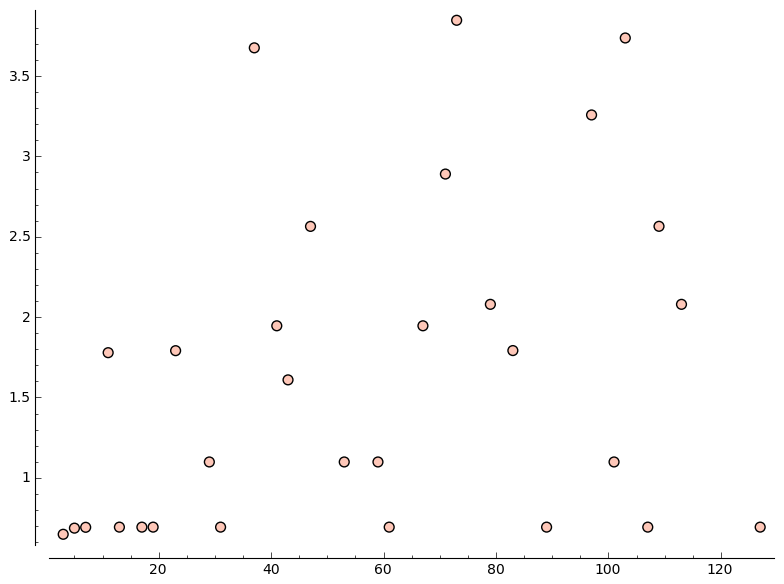
3: 0.64863671635177111430 5: 0.68679744089702920995 7: 0.69202672663694164701 11: 1.77861859937429023226 13: 0.69313778996273867072 17: 0.69314673177031971285 19: 0.69314708017307946619 23: 1.79109816372933838835 29: 1.09861201892075888153 31: 0.69314718054492396870 37: 3.67543595992579419374 41: 1.94586621625919020673 43: 1.60943632967155769720 47: 2.56444911729959734714 53: 1.09861228865934190679 59: 1.09861228866741833521 61: 0.69314718055994528623 67: 1.94590966096814188546 71: 2.89012626063473065940 73: 3.84695221418445187922 79: 2.07944120977407465034 83: 1.79175946600046365198 89: 0.69314718055994528623 97: 3.25786433053089119483 101: 1.09861228866810978211 103: 3.73682232044839146567 107: 0.69314718055994528623 109: 2.56494786625013748704 113: 2.07944153920337404529 127: 0.69314718055994528623 |
scatter_plot([(n,log(f)/n) for n,f in firsts])
|
|
from itertools import tee,product
def sum_pow(n,limit=range(10)):
for a,b in product(*tee(limit)):
p = a**n + b**n
if p in primes:
yield p
sorted(sum_pow(4))
[2, 17, 17, 97, 97, 257, 257, 337, 337, 641, 641, 881, 881, 1297, 1297, 2417, 2417, 2657, 2657, 3697, 3697, 4177, 4177, 4721, 4721, 6577, 6577, 10657, 10657] |
|
|