The third Newcastle MathsJam was yesterday. I felt last time round that it might be worth writing up what we did, both so new people can get an idea of what MathsJam is about, and also as a reference in case something comes up again in a later meeting.

First of all, I posed a problem which was first told to me by another student at Newcastle, and which I can’t find anywhere on the web. It’s called,

“Princess in a Castle.”

There is a castle with four rooms arranged in a line. Each night, the Princess picks a room to sleep in. The room she picks must be directly adjacent to the one she slept in the night before. On the first night, she can pick any room.

The Prince would like to be in the same room as the Princess (we need not ask why), but she will not tell him where she is sleeping. The Prince may pick one room each night to see if the Princess is inside. If she is, then the Prince is happy. If she isn’t, he tries again the next night.

Is there a sequence of rooms the Prince can pick to guarantee that he will eventually find the Princess?

The idea of the Prince doggedly trying to get into the non-consenting Princess’s room at night seemed a bit troublesome after discussing the puzzle for a while, so an alternate framing is to think about Dracula hiding in a castle, and Van Helsing trying to find him.

I already had a solution which I’d found by trial and error, but Andrew came up with a very convincing parity argument, which goes as follows: Number the rooms 1 to 4. The princess’s room must be of a different parity (even or odd) each night. If the Prince goes 1-2-3-4 and don’t find the Princess, at some point the Princess must have swapped places with him and ended up on his left, so when he is on odd numbers she is on even numbers, and vice versa. The Prince then needs to wait another night in room 4, and then the Princess must be in room 2.

After finding this solution, it’s natural to see if a solution can be found for general layouts of rooms.

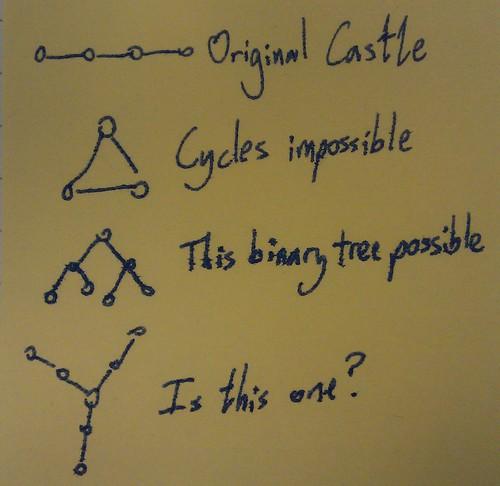
Castles with more rooms to the right of room 4 can be solved in pretty much the same way. Any layout with a cycle in it is impossible, because the Princess always has two choices of room. That only leaves trees to think about.

We found a solution for the third layout in the picture above, but think the bottom one might be impossible. Is it?

Update: I’ve been getting a pretty steady stream of people searching for the solution to this puzzle. If you’re one such, you might like to know that I’ve written an extensive post, with interactive examples, describing the solution to the general case and how we found it.

Maths in the media

After giving up on the princess-on-a-graph puzzle, we discussed maths in mainstream media – is there room for a ‘proper’ maths series on TV? Marcus du Sautoy’s The Code wasn’t very satisfying because of the awkward way it was framed. I mentioned Dara O’Briain’s new series, but is there anything else?

What about the Internet – there doesn’t seem to be one big general-interest maths site that everybody looks at. Instead, there are lots of people doing their own thing, with a lot of overlaps. I’m certainly not not part of the problem.

MathOverflow doesn’t really fit that description because it’s just for answering rather high-level questions, and the atmosphere is very competitive.

What would a big general-interest maths site look like? Is there anything similar for other subjects?

A coin puzzle

Finally, Eamonn posed this problem from a puzzle book:

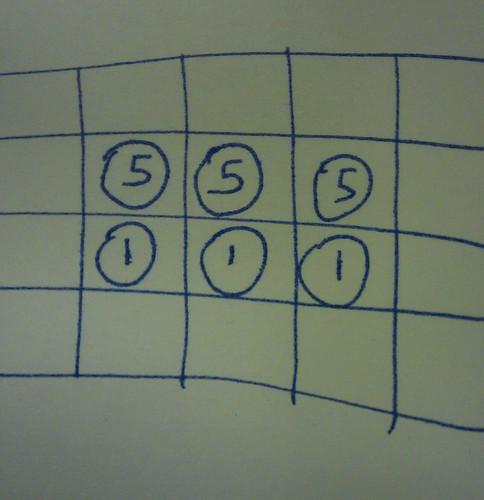
We have a 5×4 grid with three 5p coins and three 1p coins arranged in rows in the centre.

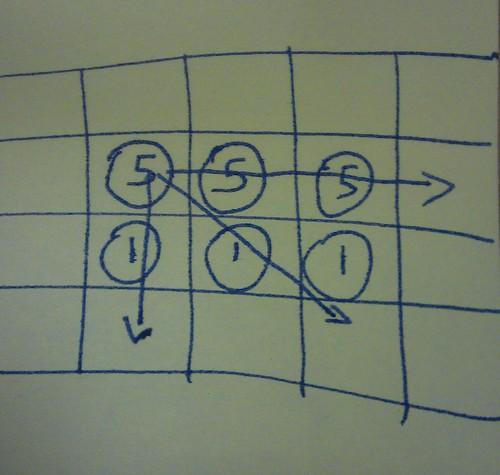
The only allowed move is to pick up a coin and ‘jump’ over one or more coins, in any horizontal, vertical or diagonal direction, to an empty square. Making several consecutive jumps with the same coin only counts as one move.

How do you swap the coins around, so the 5p coins are on the bottom and the 1p coins are on the top?

There is a solution which uses only 9 moves. It took a very long time to find. Eamonn wrote it down but I don’t have a copy.

That’s it! I had wanted to practise paper-plate folding before my PGF talk, but I didn’t get round to it.