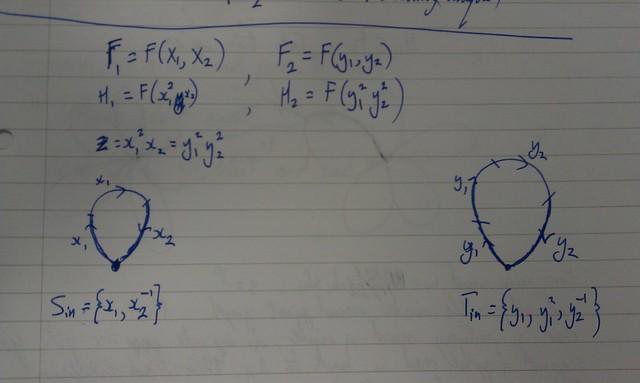I gave another presentation about Numbas last week at the e-Assessment Scotland conference in Dundee. I revised my old slides and created a better demo exam, so I thought I’d better link to them from here. I’m thinking about recording a screencast of how to use Numbas – would that interest anybody?

Anyway, those slides – click here.

I’ve started a new tumblog as a collection of maths-art intersections I find on the web. It’s at artymaths.tumblr.com.

I’ve added a lot more user-friendly features to my write maths, see maths tool over the past couple of weeks, and I’ve moved it to its own domain.

The tool is now available at http://takenot.es, which I think we can all agree is a terrifically clever domain name.

Since I last wrote about it, I’ve added the ability to save and retrieve pages, and support for automatically embedding things like pictures and videos using oEmbed

There’s also a print stylesheet, so if you print a page of notes it will look clean and tidy.

Finally, as well as HTML output you can now also get a proper LaTeX document of your notes by clicking on the “TeX please” button.

I’ve been using it to write up real notes for my research, and I’m very pleased with how quickly I can get stuff written down. I have something like TeX-anxiety for writing up maths, mainly because the process of writing a LaTeX document is such a hassle. With this tool, I can see what I’m doing as I type it, and there’s much less pressure to worry about things looking proper while I’m just transcribing thoughts.

Please have a go at using it and tell me what you think. Any suggestions for other aspects of mathematography that could be made easier with some Internet magic are also welcome.

Liza Frenkel is visiting the department, and she wants me to write an algorithm to compute double coset representation normal forms for free products with amalgamation.

Here are some notes I typed up in write maths, see maths as she and Andrew talked. I’m just putting them up here so I don’t lose them.

Suppose:
$F_1$, $F_2$ free groups (finitely generated by $X$ and $Y$, respectively)
$H_1\le F_1$, $H_2\le F_2$
$\mathrm{\exists }$ an isomorphism $\varphi :H_1\to H_2$
i.e. we have a finite generating set (in fact a basis) $\{h_1,\dots ,h_n\}$ for $H_1$ (and$\{h_1\prime ,\dots ,h_n^{\prime }\}$ for $H_2$) and generating sets $X,Y$ for $F_1$ and $F_2$

Consider a group generated by $z_1,\dots ,z_m$, with
$z_1=h_1(x_1,\dots ,x_n)=h_1\prime (y_1,\dots ,y_r),\dots ,z_m=h_m(x_1,\dots ,x_n)=h_m^{\prime }(y_1,\dots ,y_r)$
$G=F_1\underset{H_1=H_2}{\ast }{F}_2$ has presentation $⟨X,Y|h_i=h_i^{\prime },i=1\dots m⟩$
Choose a set $S\subseteq F$ such that $F_1={\displaystyle \bigcup _{s\in S}{H}_{1}s{H}_1}$
(we are assuming $S$ is infinite)
every element $w$ of $F_1$ is equal to $w=h_{1}s{h}_2$, for unique $s\in S$,
$h_1,h_2\in H_1$
can do the same for $F_2={\displaystyle \bigcup _{t\in T}{H}_{2}t{H}_2}$

Let $g\in G$.
A word $w$ representing $g$ is in normal form if $w=h_{i_1}(z)p_1{h}_{i_2}(z)p_2\dots h_{i_k}(z)p_k{h}_{i_{k+1}}(z)$, with $p_i\in S$, $i=1\dots k$.

Suppose $g=g_1{g}_2\dots g_k$. Rewrite using double coset representatives
$g=h_1(X)s_1{h}_2(Y)t_2{h}_3(X)\dots$

$g$ is in reduced form if $g=g_1\dots g_k$ and
$k=1\Rightarrow$ $g\in F_1$ or $g\in F_2$
$k>1\Rightarrow g_i\in F_1\mathrm{\setminus }{H}_1$ or $g_i\in F_2\mathrm{\setminus }{H}_2$ and $g_i$, $g_{i+1}$ belong to different factors

Let ${\mathrm{\Gamma }}_{H_1}$ be a folded subgroup graph of $H_1$. Take two copies.

For some word $w=h_{1}s{h}_2$, the question is how to find $s$.

Algorithm:
Read all possible loops round first graph, to get $h_1$.
Keep reading letters round the graph until there is no edge corresponding to the current letter. Call this $s_1$.
Start at the other end, reading loops to get $h_2$, and then maximal $s_2$ partway round a loop.
Then either there are no letters left to look at, and $s=s_1{s}_2$, or some bit $f_0$ in the middle, and $s=s_1{f}_0{s}_2$.

We want $h_1,h_2,s$ to all have maximal length.

Example

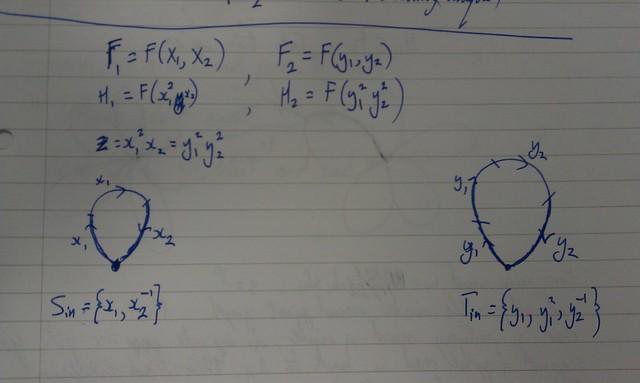
i) $\begin{array}{rl}g& =x_1^3{x}_2^2{y}_1{y}_2\\ & =(x_1^2)(x_1{x}_2)(x_2^{-1}{)}^{-1}\cdot (y_1)(y_2^{-1}{)}^{-1}\end{array}$

Membership problem

$$\begin{array}{rl}G& =F_1\underset{H_1=H_2}{\ast }{F}_2\\ H_3& =⟨c_1,\dots ,c_l⟩⩽G\end{array}$$
Can write the $c_i$ in normal form.
Question: Given $w\in G$ in normal form, is $w\in H_3$?

Constructing a folded graph which makes use of the normal form is tricky.

I’ve put the source to my write maths, see maths editor on github. The latest version should always be available there.

In other news, I’ve added support for geometric diagrams using JSXGraph. It’s good for very simple diagrams, but I don’t think you can do anything hugely complicated with it.

I’ve written a bit of javascript that uses jQuery and MathJax to make a sort-of-WYSIWYG maths editor.

Because MathJax can typeset LaTeX pretty much instantly, it’s a lot quicker to work with than the usual LaTeX write–compile–look loop.

I’m thinking about using this for videos of problem solutions. Because it’s LaTeX it’s a lot neater than my handwriting, and I don’t have to faff around with cameras.

The problem in this video is from an old P6 Further Maths A Level paper. I picked a question that wouldn’t require too much typing, but had some meat to it. If I did this properly I’d talk over it, but at the moment I’m a bit tired and the family upstairs are being quite noisy.

You can have a go on the editor here but beware that I’ve only tested it on Google Chrome. What you type gets saved to your browser’s local storage, so it should persist between browser sessions.

What do you think about it? Is it helpful? Would you consider using something like it?

I’ll try and make this my last Numbas post for a while, but I’ve had to give a few presentations about Numbas at various places in the past month, so I wrote a quick set of slides. I’ve just uploaded it here.

I created the slideshow using Slidy, which is much better at using HTML for slideshows than my attempt.

Numbas, my web-based e-assessment system, is now available under an Apache 2.0 licence at github. That means it’s finally properly open-source, and anyone can do whatever they like with it.