Liza Frenkel is visiting the department, and she wants me to write an algorithm to compute double coset representation normal forms for free products with amalgamation.

Here are some notes I typed up in write maths, see maths as she and Andrew talked. I’m just putting them up here so I don’t lose them.

Suppose:
$F_1$, $F_2$ free groups (finitely generated by $X$ and $Y$, respectively)
$H_1\le F_1$, $H_2\le F_2$
$\mathrm{\exists }$ an isomorphism $\varphi :H_1\to H_2$
i.e. we have a finite generating set (in fact a basis) $\{h_1,\dots ,h_n\}$ for $H_1$ (and$\{h_1\prime ,\dots ,h_n^{\prime }\}$ for $H_2$) and generating sets $X,Y$ for $F_1$ and $F_2$

Consider a group generated by $z_1,\dots ,z_m$, with
$z_1=h_1(x_1,\dots ,x_n)=h_1\prime (y_1,\dots ,y_r),\dots ,z_m=h_m(x_1,\dots ,x_n)=h_m^{\prime }(y_1,\dots ,y_r)$
$G=F_1\underset{H_1=H_2}{\ast }{F}_2$ has presentation $⟨X,Y|h_i=h_i^{\prime },i=1\dots m⟩$
Choose a set $S\subseteq F$ such that $F_1={\displaystyle \bigcup _{s\in S}{H}_{1}s{H}_1}$
(we are assuming $S$ is infinite)
every element $w$ of $F_1$ is equal to $w=h_{1}s{h}_2$, for unique $s\in S$,
$h_1,h_2\in H_1$
can do the same for $F_2={\displaystyle \bigcup _{t\in T}{H}_{2}t{H}_2}$

Let $g\in G$.
A word $w$ representing $g$ is in normal form if $w=h_{i_1}(z)p_1{h}_{i_2}(z)p_2\dots h_{i_k}(z)p_k{h}_{i_{k+1}}(z)$, with $p_i\in S$, $i=1\dots k$.

Suppose $g=g_1{g}_2\dots g_k$. Rewrite using double coset representatives
$g=h_1(X)s_1{h}_2(Y)t_2{h}_3(X)\dots$

$g$ is in reduced form if $g=g_1\dots g_k$ and
$k=1\Rightarrow$ $g\in F_1$ or $g\in F_2$
$k>1\Rightarrow g_i\in F_1\mathrm{\setminus }{H}_1$ or $g_i\in F_2\mathrm{\setminus }{H}_2$ and $g_i$, $g_{i+1}$ belong to different factors

Let ${\mathrm{\Gamma }}_{H_1}$ be a folded subgroup graph of $H_1$. Take two copies.

For some word $w=h_{1}s{h}_2$, the question is how to find $s$.

Algorithm:
Read all possible loops round first graph, to get $h_1$.
Keep reading letters round the graph until there is no edge corresponding to the current letter. Call this $s_1$.
Start at the other end, reading loops to get $h_2$, and then maximal $s_2$ partway round a loop.
Then either there are no letters left to look at, and $s=s_1{s}_2$, or some bit $f_0$ in the middle, and $s=s_1{f}_0{s}_2$.

We want $h_1,h_2,s$ to all have maximal length.

Example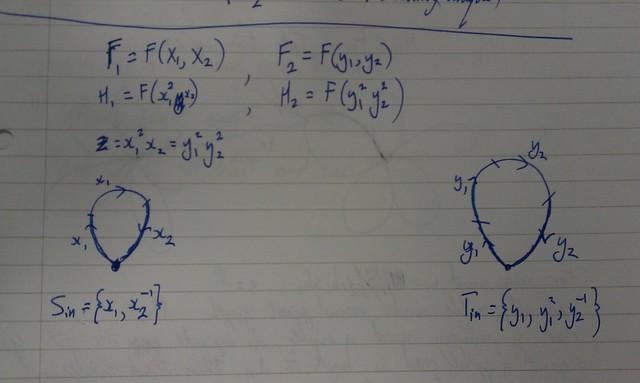

i) $\begin{array}{rl}g& =x_1^3{x}_2^2{y}_1{y}_2\\ & =(x_1^2)(x_1{x}_2)(x_2^{-1}{)}^{-1}\cdot (y_1)(y_2^{-1}{)}^{-1}\end{array}$

Membership problem

$$\begin{array}{rl}G& =F_1\underset{H_1=H_2}{\ast }{F}_2\\ H_3& =⟨c_1,\dots ,c_l⟩⩽G\end{array}$$
Can write the $c_i$ in normal form.
Question: Given $w\in G$ in normal form, is $w\in H_3$?

Constructing a folded graph which makes use of the normal form is tricky.