It’s been two months since I last wrote one of these! March was a haze of overwork and stress for me, so I didn’t write a recap for March’s MathsJam while it was still March. Peter Rowlett, who was visiting Newcastle as part of his mission to avoid having to think up new puzzles for MathsJams by always attending different ones (and also to give a talk at the university) has kindly sent me his notes, so here’s what I’ve reconstructed:

Big noughts and crosses

I have this picture of Naomi playing noughts and crosses on a big board. I can’t remember what the rules were. A different version by David Cushing swept round the Newcastle maths department for a while until we proved it had ambiguously-won games. I won’t bother writing up the rules for that version.

 

Dice

Somebody asked if you can make two dice, with different sets of numbers on their faces, so that when you roll them both the sum will have the same probability distribution as two normal dice? An additional constraint is that only positive numbers are allowed.Somebody at another MathsJam tweeted a picture of just such a pair of dice, and @outofthenorm2 tweeted a nicely-rendered diagram of the solutions to the puzzle.

 

Mad Abel

We played Mad Abel again. Here’s a picture of Peter losing.

Poker

Matthew Taylor outed himself as a former president of Durham’s Poker society and suggested a two-player game involving poker hands. You deal out four piles of five cards, face-up. Players take turns to take the top card of one of the piles into their hand. When all the cards have been taken, the players’ hands are judged as poker hands. I can’t remember if anyone came up with a strategy for this.

 

An almost-Collatz game

David Cushing made a hero’s return to MathsJam with a fun number theory game that I don’t think anyone quite got round to solving. I enjoyed it regardless.

• Both players agree on an upper bound, for example 100.
• The first player writes down a whole number lower than the upper bound.
• Players take turns writing down either a factor or a multiple of the previous number. Numbers can only be picked once per game.
• The first person not able to pick a number (because all of the previous number’s factors and multiples have been picked) loses.

Matthew was doing something with graphs of possible moves but I don’t think he managed to solve the game.

 

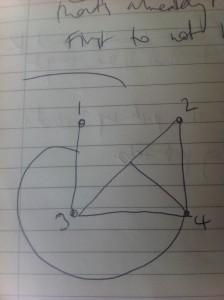
Baffling graph theory

(or graffling bath feary)

Peter has sent me a photo of a game I must have missed because it’s completely baffling. Apparently you draw $N$ points and label them with the numbers $1\dots N$. The challenge is to draw edges such that each point is joined to as many edges as its label. An edge can start in the middle of another edge, but only once per edge.

A variation is to draw $N$ points, all with the label $N$. $1$ is a loop, $2$ is a triangle, and $3,4,5$ are also possible. Peter asks if any larger numbers are possible.

We played with the zero-magic graphs from Samuel Hansen’s thesis. Peter had a sketchpad full of festively shaped graphs produced while trying to make last year’s Christmas cards.

 

Bulletin of the British Society of Hysterical Mathematicians

Peter brought an issue of the BSHM Bulletin which prompted a discussion of the 15-game and when it is solvable.

 

Jeff Weeks’s Torus Games

David brought in his iPad and showed us a game which lets you play pool on a torus. There was much confusion about shot placement.

 

I had a bit of a discussion with John about HyperRogue, a roguelike game played in hyperbolic space. We both wanted to make something like a hyperbolic orienteering game, where the negative curvature of space messes with your ability to follow directions.

That’s all I’ve got for March. Sorry this wasn’t a proper post. April’s is really good though, so hopefully that makes up for it.