I’m editing a paper (12 months and counting!) and I’ve had a few thoughts about LaTeX that I thought I’d write down. I don’t even care if this makes me a neckbeard, that’s the mood I’m in currently.

The hyperref package makes your references clickable when you compile to PDF. I can’t think of a reason not to use it.

I dislike people who set their editors to have a fixed maximum line-width! Word-wrap works fine, and means the window is full no matter how big it is. Also, newlines can be used to separate thoughts more clearly.

Avoid eqnarray.

I noticed that a remarkable number of words starting with gr are still words if you swap the gr for h. For example, the words in the title of this post. How many words is this true for? Which pair of prefixes has the most words in common?

Here’s a Python script I wrote to answer those questions. Here’s the list of words I used. And here are the results. I only looked at prefixes of one or two letters.

The best pair was no and u. Here’s the list of suffixes they have in common. Most of it is words which can be prefixed with un or non. That isn’t very interesting, so I think the real winner is (b,st), with 1085 suffixes in common. It’s the first pair where one of the prefixes is two letters, and where most of the words aren’t just words with another Latin prefix in front of them.

I could do loads of calculations like this. If you import the Python script as a module, you can have a look at all the data it computes. Very interesting!

The word list I used probably skewed the results quite a bit because it contains lots of words which are conjugations or pluralisations or whatever of the same root word, as well as a load of really weird words which probably occur once in the whole corpus. I think if I look at this again I’ll use something like this frequency list, and use the frequencies of words as a weighting for scoring prefix-pairs.

I’ve been annoying Nathan with these all week.

Why is $D_6$ better for the environment than $Z_6?$ Because it doesn’t commute.

Which bit of Jessop’s does René Descartes like best? The Konica section.

What goes well with a curry and can compute any recursive function? NAND bread.

A colleague claims to know the secret recipe for authentic Coca-Cola. How does he proves this to you without revealing the recipe? With a zero-knowledge protocola.

In the Music Hall of Fame, which guided visit takes you from James Brown up to George Clinton in the quickest time, but is best enjoyed while under the influence? The add-joint funk-tour.

So I was just making my dad’s birthday card. I felt it would benefit from some typography, so I got out a sheet of letter transfers I bought a while ago.

Something immediately leapt out at me: where are all the Es? As anyone who was a bit obsessed with cryptography when they were young knows, the most common letter in English is E, by a long way, and there are hardly any Qs, Xs or Zs. This fact has helped us (and our enemies) win wars.

So, here’s a graph of the relative letter frequencies on the sheet compared to the frequencies in the English corpus (from Simon Singh’s site):

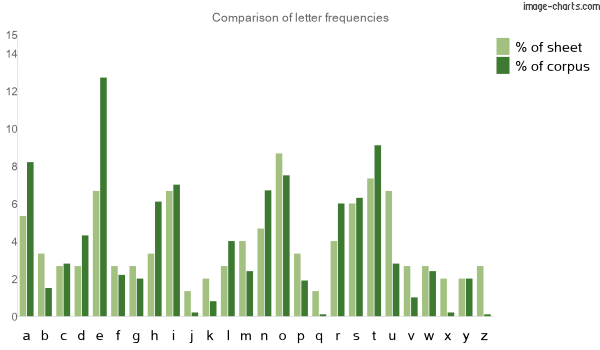There are about half as many Es as there should be and loads more Qs, Xs and Zs than I will ever use. Now, the sheet’s quite small, so a statistician would do a hypothesis test to see if there is a significant difference between the sheet and the corpus, but I’m not one of those so I’m going to stop here, outraged at WH Smith’s lack of rigour.

I suppose if they’d only put one Z in people would worry about a situation in which they needed to use two Zs, while it isn’t as immediately apparent that there aren’t enough Es to make use of the whole sheet.

The upshot is, I think my dad’s card is going to have to have somebody sleeping in a queue for a xylophone quorum, in order to get the most out of this sheet. My hands are tied by Statistics.

PS It isn’t all bad though – there are twice as many 1s as any of the other non-zero digits, so it at least makes a nod to Benford’s Law.

I've started a collection of interesting non-pregroup-related papers on Mendeley. At the moment this includes a formal system which makes the diagrams in Euclid's proofs a part of the formal reasoning, and "How to explain zero-knowledge protocols to your children"