I think it’s only been a month since my last Newcastle MathsJam recap but I’m sure I’ve forgotten how to write one. Here goes.

There were eight of us in November, including two very welcome new Durham undergrads.

John began with a printout of Brent Yorgey’s factorisation diagrams. Several people battled against the poor pub lighting to try to discern the scheme behind the colouring.

Ji briefly mentioned a puzzle from his coding theory course – how to weigh twelve balls on a set of scales in the fewest weighings? I don’t have the answer written down, and I won’t work it out! The puzzle might actually be to separate one light ball from the uniformly-heavy others. I can’t remember.

Katie, organiser of Manchester MathsJam, had asked the organisers of all the MathsJams around the world to fill in a survey so we can get an idea of what’s going on everywhere else. There were a couple of Fermi-problem type questions at the end, asking for estimates of how many ping pong balls would fit in our pub, and how many dominoes were in a bag in a photograph. Our answers were, respectively, “probably quite a few”, and “exactly 253”, both calculated by taking arithmetic means of everyone’s guesses. I’m definitely going to fill the rest of the survey in after I finish this post. Definitely.

Someone at another MathsJam tweeted this question:

Two robots land at random locations on a sphere. What identical path should they both follow so they collide?

We couldn’t think of an answer that made sense, apart from “inwards”.

Eamonn had bought a compendium of Puzzlebombs at the big MathsJam conference. It includes a sneaky preview copy of December’s sheet, which includes a puzzle by me, CP! After lots of reassurances that it wasn’t as hard as it could’ve been, a few people cracked it.

Picture-hanging

Following my recreational maths seminar on the subject, I thought I’d pose the picture-hanging puzzle in real life:

How do you hang a picture from $n$ nails so that removing any one nail causes the picture to fall?

I demonstrated the solution on two nails a few times, using empty glasses as stand-ins for nails. A couple of people got it fairly quickly. Amazingly, Andrew said he already knew the solution because he’d solved basically the same problem in a serious knot theory paper.

Here are Andrew and Ji making their attempts:

I’ve had quite a few goes at the 5-nail puzzle and I haven’t got it to work yet. 2,3 and 4 were all straightforward, so I must be doing something wrong. Maybe I’ll work it out.

I showed everyone the Wow-Card that Mark Carney gave me at the big MathsJam. Everybody was suitably impressed. Marjane claimed to have worked out how it was made, but I’m not sure.

Eamonn had brought a pack of Set cards, so we played a few games. Andrew was way, way better than the rest of us. I pled colour-blindness.

Car-sharing puzzle

I’ve had this puzzle saved in my “things for MathsJam” file for ages and ages. I finally used it:

My brother Morty and I took a drive up to the mountains this weekend to see the Golden-breasted Flooglebird. Morty drove the first 40 miles and I drove the rest of the way. We saw the Flooglebird right away (or something closely resembling it) and immediately returned home on the exact same route.

On the return trip Morty again drove the first part of the trip, and I drove the final 50 miles this time.
In total who did the most driving, me or Morty, and how many more miles than the other brother did that driver do? (yes, there’s enough information to reach an answer!)

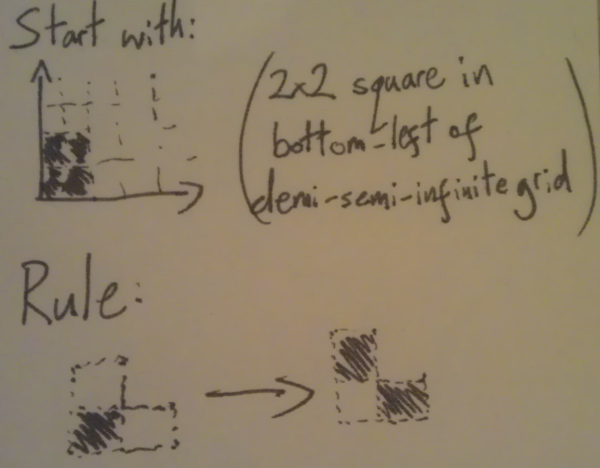
Ji’s cellular-ish automaton

Ji asked us a question about a rule on patterns on a grid. The setup goes like this:

Take a demi-semi-infinite grid (or the top-right quarter of an infinite grid, if you like) and fill in the $2\times 2$ square in the bottom-left. The Rule is that, whenever you have an (oriented) L-shape with the corner filled in and the ends empty, you can swap it for an L-shape with the ends filled in and the corner empty.

Ji’s question was: what patterns can you make in the bottom-left $2\times 2$ square? I quickly found a couple of patterns that Ji reckoned couldn’t be done, but there are 16 possibilities. Andrew came up with a rather marvellous argument that some patterns are impossible.

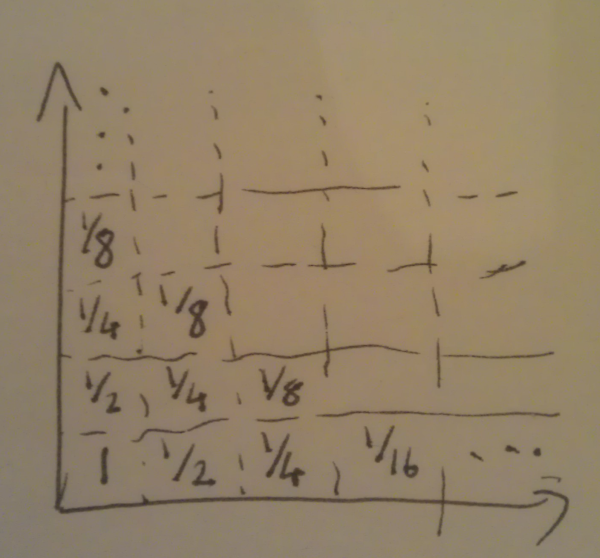
Write numbers in each of the squares, starting with $1$ in the bottom-left corner, $\frac{1}{2}$ in the squares next to it, and further powers of $\frac{1}{2}$ in the rest of the diagonals. So the bottom row of the grid reads $1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\dots$. The sum of the whole grid is exactly $4$. I worked this out by summing the rows individually, but I think Andrew got there a different way, or it just looked like it should be 4.

The sum of the filled-in squares is an invariant across all patterns. That’s because the squares above and to the right of a square labelled $x$ are both labelled $\frac{x}{2}$, so when you apply the Rule to the square $x$, you take away $x$ and add $\frac{x}{2}+\frac{x}{2}=x$. So no matter how many times you apply the Rule in whatever order, the filled-in squares will always add up to the same amount.

At the very start, the sum of the filled-in squares is $1+\frac{1}{2}+\frac{1}{2}+\frac{1}{4}=2\frac{1}{4}$. That’s more than half of the available score so no matter what you do, you can’t end up with the bottom-left square completely empty. QED!

Eamonn presented us with the Movie Math Quiz from Spiked Math. I don’t like it.

Finally, I have in my notes that we talked about space-filling curves. I can’t remember why!

I enjoyed myself, as always. We decided December will be a non-MathsJam month, because we have better, more turkey-oriented, things to be doing. The next Newcastle MathsJam will be on the 22nd of January, TWENTY THIRTEEN!