February’s MathsJam was loads of fun! We had a record attendance of 14 cheery people who just about managed to fit around the biggest table in the Charles Grey.

After last month’s puzzlocalypse, which left me for over a week unable to count the toes on my feet, I wanted to have a nice relaxed evening.

Matthew Taylor began proceedings with a puzzle which is apparently setting Durham alight (there isn’t much to do there).

Two fat ladies and all the threes

Using each of the numbers $8,8,3$ and $3$ exactly once but in any order, along with the arithmetic operations $+,-,\times ,÷$ and brackets, can you make $24$?

$8\times 3=24$ isn’t a solution because it only uses two of the numbers.

Have a proper think about this – it’s just a brainteaser, so anybody should be able to solve it by just scribbling for a while.

Click here for the solution

Eamonn brought a copy of the latest UK Maths Challenges. He and Sarah set off solving those. Sarah thrashed me in the Maths Challenge when we were in school together and she was out to repeat the feat.

There were some quite fun questions on the Team Challenge but I’m probably not allowed to repeat them here. Find a friend who is a teacher and get a copy!

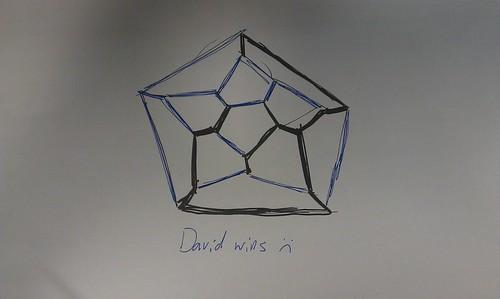
A few of the Durham people had noticed a tweet I posted last week about a game David Cushing invented:

David’s edge-picking game

David’s new game: take turns choosing edges. First to pick a cycle loses. What happens when it’s played properly? — Christian Perfect (@christianp) February 14, 2012

It’s a generalisation of the game Sim to graphs other than the complete graph. In the picture above, we played on a dodecahedron.

The players each pick a colour and then take turns to colour in edges with their colour. If a player colours in an edge which completes a cycle of their colour, they lose. A cycle is a closed path along the edges.

We don’t know what the optimal strategy for the game is. I’ve tried to encourage David to read Winning Ways for your Mathematical Plays to get some tools for attacking the problem, but so far he has demurred.

I don’t know if anyone had any grand insights at MathsJam – I was trying to keep up with what the Durham people were talking about but I was distracted by other things. I rescued this bit of paper at the end of the evening:

Can anyone post some thoughts in the comments?

Meanwhile, stand-up mathematician Matt Parker and others were trying at the opposite end of the table to draw all the stars with $n$-fold symmetry that it is possible to draw without lifting your pen off the paper.

I don’t know what the result of that effort was. Anyone?

Eamonn told me a problem which he’d been told by someone and I’d been told by someone else, but I couldn’t remember the answer.

Chopping up Rubik’s cube

You are given a solid cube. How many chops through the cube do you need to make to split the cube into 27 smaller cubes of equal size? You may rearrange the pieces in between chops.

There’s an obvious upper bound, but we couldn’t decide if it could be done in fewer moves. Tash told us the answer very quickly after being told the problem.

Click here for the answer.

On another trip up to the other end of the table I learned that people were working on a hats puzzle.

Yet another hats puzzle

$10$ prisoners are each told the following:

• A guard will put a hat on you. The hat will have a number on it. The number can be any real number – positive, negative, $\pi$, the Champernowne constant, whatever.
• You will be led into a room where you can see the numbers on the other prisoners’ hats but you can not see your own.
• Without communicating, you must each put on either a black or a white shirt so that when you are lined up in order of the numbers on your hats, your shirt colours alternate.
• Before all of this, you can confer and agree on a strategy.

I was going to introduce this as a particularly unintuitive hats puzzle but, really, they’re all this bad.

Just before I went to MathsJam I was shown a very nicely written-up solution of this puzzle which the author is going to publish fairly soon, so I won’t bother writing a solution here. It was odd to see it again so soon!

Rob Botcherby found the solution at MathsJam but he didn’t know why it worked. It’s a very pleasing solution when you do find it.

Another product of the prison-ludological complex was presented by Eamonn.

Cell Block 8

In a prison there is a block of 100 locked cells, each with a prisoner inside and a guard stood outside.

Starting at cell $1$, each guard moves down towards cell $100$, locking cells that are unlocked and unlocking cells that are locked. After the final guard has reached the end of the block, which cells are unlocked?

I’ve been told this sort of puzzle framed in a few different ways before. I don’t think I can do any better explaining the solution than James Grime, so I’ll just embed his video here.

What I’d really been looking forward to doing at this month’s MathsJam was playing the game Mad Abel.

Mad Abel

I’ve been meaning to play Mad Abel ever since the first Newcastle MathsJam last August but I always got distracted by other things. There was also a tiny worry in my mind that there might still be some very old laws on the books about playing cards in pubs.

Anyway, I decided after last month’s intellectual war of attrition that what we needed was to play some games, so I brought a couple of decks of cards and a set of the rules.

Mad Abel is a card game invented by Smári McCarthy based on abelian groups. The rules I linked to above are pretty easy to understand, though I recommend you try the version with five cards per suit first.

It’s a huge amount of fun to play, and the rules are surprisingly easy to get your head round in a couple of minutes. For a while Mad Abel fever swept the room and everybody was either playing or advising somebody else on how to play.

A few questions arose:

• is it possible to deal out all the cards and have neither player able to make the target sum?
• does every game eventually end, or can you get stuck in a loop?

I reckon the first of those questions can probably be answered fairly straightforwardly. We need a finite group theorist!

I’m going to record a video about the game when my cold-induced nasality has gone away.

Chris Dickson brought some rather excellent physical puzzles with him. The first was this gem:

The idea is to fold the blocks round so that they read like a properly-formed sum.

Click here to see the solution.

Chris also bought some octiamonds. They’re a bit like the Lominoes we played with last month – they’re all the shapes you can make from eight equilateral triangles.

Sadly, Chris tells me he’s missing one of the orange pieces, so if you find you’ve got it please let me know.

All of a sudden, people started doodling knots. I’m not sure what prompted it, but I learned some fun things.

Some very interesting maths started happening when Matt and others tried to find out how many line doodles you can draw with a certain number of crossings.

Somebody must have thought of looking at this before. I wonder if anyone’s got a solution?

Naomi showed us a proof-by-doodle of a nice little fact: if you draw a closed loop with your pen, going underneath the existing line when you cross it, it’s always equivalent to the unknot.

A physical demonstration of spooling Chris’s shoelace onto the table convinced any who remained doubting.

Someone posed a topical problem, similar to Andrew Lobb’s question last month about money in brown envelopes.

Golden-brown pancakes

There are three pancakes. One is brown on both sides, one is golden on both sides, and the last is brown on one side but golden on the other.

A pancake is chosen and flipped a random number of times. You can see that it’s brown on the top.

What’s the chance that it’s brown on the other side?

I wasn’t on the night, but I’m fairly sure now that I agree with Andrew and Rob about the answer to this one, but maybe we can have an angry discussion in the comments if anyone thinks the answer isn’t $\frac{2}{3}$.

I spent an embarrassingly long time trying to remember Bayes’ Theorem.

There was some discussion of how many regions you can chop space into with $n$ planes. A few people knew the answer for chopping up two-dimensional space with lines but, as ever, adding an extra dimension scuppered a lot of things.

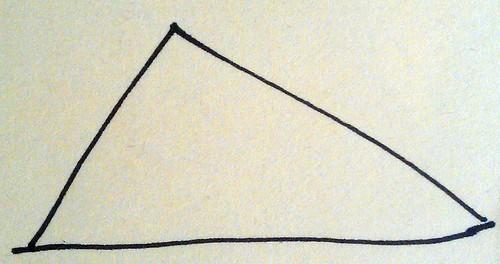
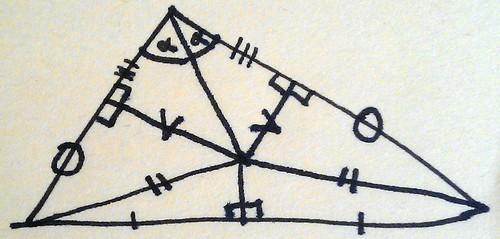
Just before we finished for the night, Andrew told us a story about triangles. I’ll try and repeat it here.

Once upon a time there was a triangle, not too fat, not too thin.

Draw any random triangle.

(Andrew took two goes at drawing a sufficiently random triangle. I mentioned I’d seen some discussion of what people draw when they say they’re drawing random triangles)

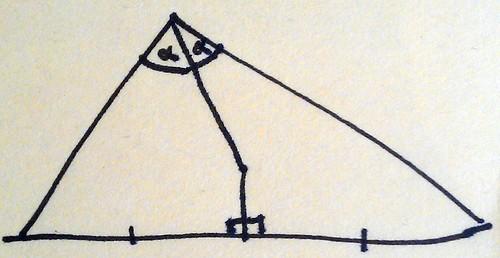
Draw the angle bisector of one of the angles and join it up with the perpendicular bisector of the opposite edge.

Now drop perpendiculars from the other two edges to the intersection point.

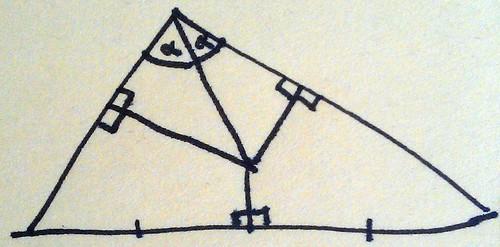
Draw lines from the other two vertices to the intersection point.

Now, because the bottom two triangles share a side and have bottom edges of the same length, their hypotenuses are equal.

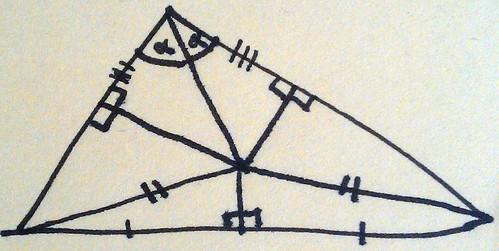
You can do the same thing with the top two triangles as well because they share a hypotenuse and have two equal angles.

In fact, you can go round finding equal lengths all over the place.

So all triangles are isosceles!

Click here if this strikes you as odd.

I had a really good time at this MathsJam. It was good to see some new people as well as the regulars. I’d like to thank everyone for coming, and encourage anyone who hasn’t been yet to come next month!