Newcastle MathsJam November 2011 recap

2011-11-23

Phew!

November’s MathsJam happened last night, and I’m totally pooped. We had a record twelve attendees and did absolutely loads of maths – so much that I ran out of space in my little notebook.

We were joined by Matt Parker (@standupmaths) who brought some of James Grime’s non-transitive dice (available from MathsGear) with him. They’re fun! Sadly, an attempt to demonstrate one die reliably beating another resulted in a draw. Undeterred, Matt did his best Ronco sales pitch about the many features of the dice. Maybe they should be called “Also!” dice.

We tried a few circle-geometry puzzles. The first one was called,

“The Pizza-Cutting Puzzle”

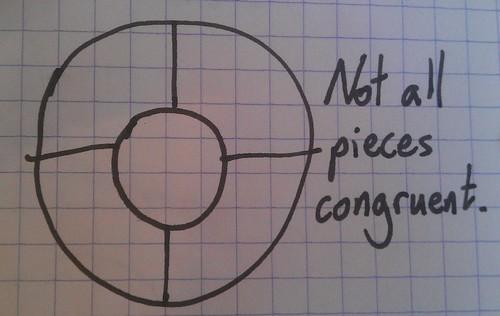
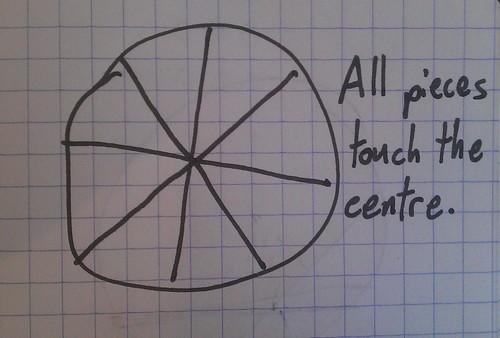
Can you cut a circle into congruent pieces so that at least one piece doesn’t touch the centre of the circle?

Here are some pictures to explain the kind of things that aren’t allowed:

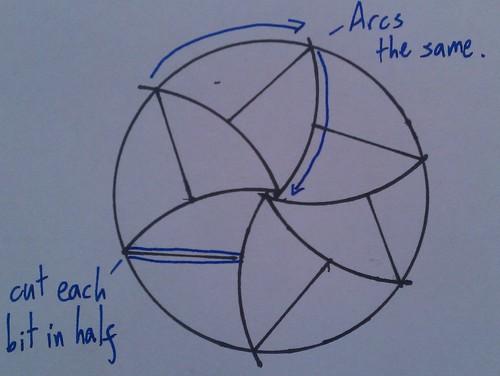
The solution goes as follows, thanks to Eamonn:

draw a circle using a set of compasses
pick a point on the circle
with the compasses set to the same width, put the pointy end on the point you picked and draw an arc connecting the centre of the circle to the edge
put the pointy end where the arc you just drew touches the edge of the circle
repeat steps 3 and 4 until you’ve gone all the way round the circle and divided it into six bits
divide each bit in half along its line of symmetry

Now you’ve split the circle into twelve congruent pieces, of which six don’t touch the centre!

It turns out that this solution has links to Reuleaux polygons! The solution I gave above uses Reuleaux triangles, but you can make other solutions by repeatedly tracing round just over half of any Reuleaux polygon, repeatedly. Matt Parker did this with a 50p piece (which is a Reuleaux heptagon)

The second circle puzzle didn’t have a name, I don’t think, so I’m going to call it

“The Unexpected Surd Identities Puzzle”

for reasons which will become apparent.

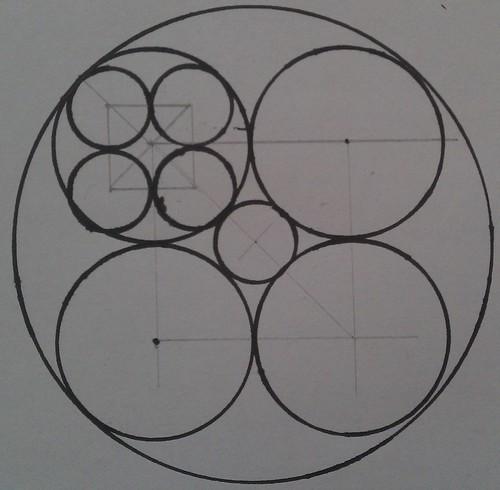
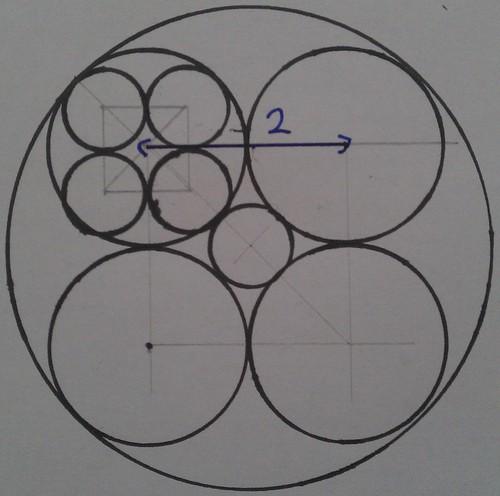
Inscribe four medium circles in a big circle so that they’re all tangent to each other and the big circle. Do the same thing for each of the four medium circles. Also draw as big a circle as you can in between the four medium circles. Is the circle in the middle bigger or smaller than the circles inside the medium circles?

I got a solution to this one pretty quickly. It’s tempting to try to work everything out in terms of the radius of the big outer circle, but that’s making things hard. Instead, declare that the radius of the middle circles is $1$ unit.

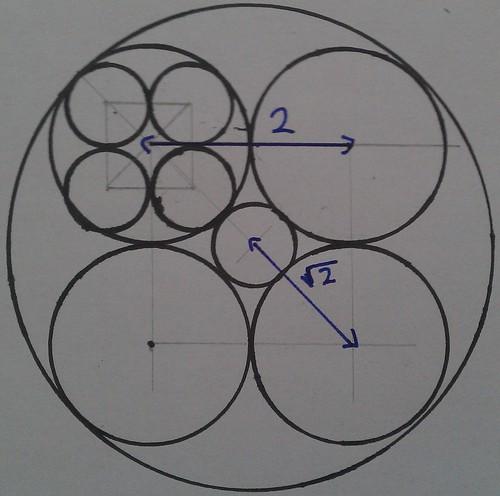
Now, the square drawn by connecting the centres of the middle circles has sides of length $2$ , because they’re two radii touching end-to-end.

Straight away, using Pythagoras, you can work out that the length of the diagonals of the square is $\sqrt{2^{2} + 2^{2}} = \sqrt{8} = 2 \sqrt{2} .$

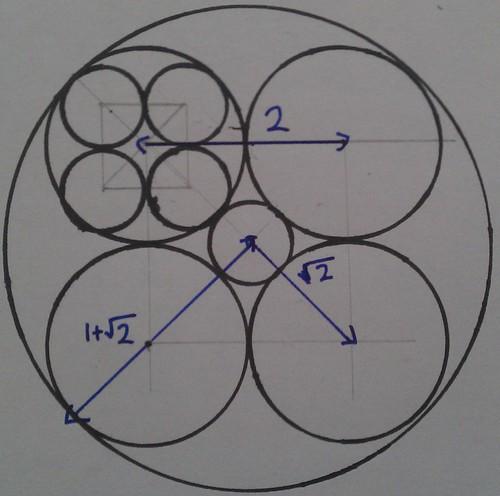
The distance from the centre of the picture to the centre of one of the middle circles is half that, so $\sqrt{2}$ .

If you carry on along that line to the edge of the big circle, you travel another unit, so the radius of the big circle is $\sqrt{2} + 1$ . That means that when you inscribe four circles in a bigger circle like we did, the ratio of the radius of the inscribed circles to the radius of the outer circle is $1 : (1 + \sqrt{2})$ .

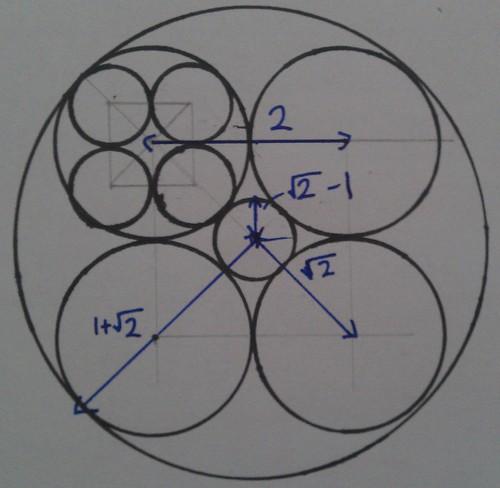
That means that the radius of the small circles inscribed in the medium circles is $\frac{1}{1 + \sqrt{2}}$

Now we’re left with the small circle in the middle of the picture. We already know that the line from its centre to the centre of a medium circle has length $\sqrt{2}$ , so if we take away the radius of the middle circle we get the radius of the small one, which is $\sqrt{2} - 1$

So which small circle is bigger? The answer is annoying: $\frac{1}{1 + \sqrt{2}} \cdot (\frac{\sqrt{2} - 1}{\sqrt{2} - 1}) = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1.$

They’re the same!

I’m getting a bit tired of writing out solutions to puzzles now, so here are just a few statements of puzzles:

The answer is $21$ . A rumour emerged that somebody had found $22$ but it appears to be baseless.
Why are all squares of primes one more than a multiple of 24? Andrew Lobb had a wonderful proof of this, which he might post in the comments.
What is the biggest integer with distinct digits whose English name has all words starting with the same letter? (American naming system allowed and, just this once, encouraged)
Matthew (who isn’t Matt) found very short solutions to the “Princess in a castle” puzzle from last month: $2332$ solves the four-door puzzle, and $23223$ solves the five-door puzzle.

Andrew Lobb came up with a good question:

“What is the narrowest part of the UK?”

Everybody pretty much immediately said something like “the tip of Cornwall”, or some other jaggy bit on the edge. This wasn’t a very satisfying answer because you can pick arbitrarily narrow bits of land using that logic.

So it was agreed that a definition of narrowness was needed, and it would have to involve a compromise between the length of the line of narrowness and the ratio of the areas of the land on either side. I don’t think we got any further than that.

NP-hard news

NP-hardness came up twice! First of all, David asked if, given advance knowledge of the pieces that will fall in a game of Tetris, whether it’s possible to work out a strategy that means you don’t lose. My encyclopaedic knowledge of esoteric mathematics gave the answer: it’s NP-hard.

As Matt was leaving, he mentioned that flipping pancakes is NP-hard.

Talking of hard problems: I mentioned the world’s shortest explanation of Gödel’s theorem.

Prisoners in hats

Many, many logic puzzles involving prisoners or hats or prisoners in hats were discussed. I can’t remember what they were, but I think we covered all of them.

Actually, I can remember one of them, which I think Tash posed, claiming that nobody manages to work out the answer before looking it up.

100 prisoners are locked in a room. In the room next-door are one-hundred boxes containing the names of the prisoners, one for each prisoner. The prisoners are taken one at a time into the room and allowed to open up to fifty boxes. If a prisoner opens the box with their name, they are set free, otherwise they are sent back to their cell. The room is put back how it was after each prisoner leaves. The prisoners are allowed to decide on a strategy before they begin. How do they maximise the chances of everyone being set free?

As promised, none of us worked it out. The solution’s quite clever! Maybe look it up!

Gray codes and the Towers of Hanoi

Gray codes have an interesting link to the Towers of Hanoi puzzle. I don’t think we added anything to what’s on the Wikipedia page, but it was very interesting.

Finally, a few card tricks were demonstrated but I wasn’t following along. Can anyone describe them?

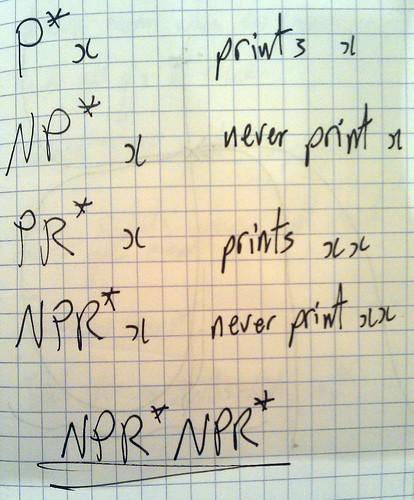
Comments

David

2011-11-24 11:20:25

23223 is not a solution of the 5 door princess in a castle. I dont think that a 5 move solution exists for the 5 door puzzle but I am probably wrong since i thought a 4 move solution did not exist for the 4 door problem.

Andrew Lobb.

2011-11-24 16:46:04

Hi – Here’s the solution to the squared primes congruence mod 24 puzzle. I don’t know if it’s ‘wonderful’ exactly – just a lesson that if your expression factorizes, you might as well factorize it. The main point is that:

$p^{2} - 1 = (p + 1) (p - 1)$

Let $p$ be a prime bigger than $3$ . So $p$ is odd and not divisible by $3$ . Hence either $p - 1$ or $p + 1$ /is/ divisible by $3$ . Also, both $p - 1$ and $p + 1$ are even and differ by $2$ , so once of them is divisible by $4$ , and the other divisible by $2$ .

Hence you see that $p^{2} - 1 = (p + 1) (p - 1)$ is divisible by $3 \cdot 4 \cdot 2 = 24$ .

Another factorization that’s interesting is $a^{2} + b^{2} = (a + i b) (a - i b)$ (you need to allow yourself to use complex numbers though)! This factorization can be used to give a nice quick proof of the (unbelievable when it is first suggested to you) fact that any prime number congruent to $1$ modulo $4$ is the sum of two squares. $5 = 4 + 1$ , $13 = 9 + 4$ , $17 = 16 + 1$ , $29 = 25 + 4$ , $37 = 36 + 1$ , $41 = 25 + 16$ , $53 = 49 + 4$ , … The details are in the introduction to Neukirch’s book on Algebraic Number Theory, and should be possible to understand with an undergraduate algebra course.

christianp

2011-11-24 16:54:20

Thanks for that. I suppose I used the word ‘wonderful’ because it was so much simpler than the other solution.

By the way, you can use LaTeX in comments here for nice maths. I’ve edited the above for you.

Matthew Taylor

2011-11-24 23:11:44

Nice writeup sir; as has been pointed out, 23223 was not a solution for the 5-door variant but rather a lengthier solution for the 4-door variant that was improved upon later.

I would hypothesise that the shortest guaranteed solution for an n-door variant with n larger than two is 2n – 4; eg. for 5, use 234432 – for 6, use 23455432 etc. Maybe that’s one for December!

Matthew Taylor

2011-11-24 23:24:21

Also, before I forget, the narrowness problem was really interesting and kept me thinking through the next day or two. I couldn’t get past the idea that I felt like you needed to define it in terms of an arbitrary bound dependant on the person wanting to know the answer – ie. people’s definitions of “satisfying”, in the sense used in the writeup, will differ.

The best idea I could come up with was that the condition on the narrowness is that in a neighbourhood around each of the two “coastal” points that give the narrowest bit, there is no line connecting two other points from the neighbourhoods that is shorter. But it’s tricky and without imposing some lower bound on the narrowness, I think every definition is going to have some unsatisfactory answers. 🙁

Aaron

2011-11-25 12:50:24

My (<140 character) answer to the square primes problem as tweeted by @standupmaths (3 Oct)

All primes ≥5 are of form 6n±1, giving square 12n(3n±1)+1. Either n or (3n±1) must be even hence divisibility by 24.

Also I was in the year above Andrew Lobb at school, assuming it's the same Andrew (given his talent at maths I'm sure it must be).

Andrew Lobb.

2011-11-26 15:47:59

I had a further thought about the narrowness problem. So say we want a narrowness function which given a chord of some plane shape gives you a real number, and we say that we want to minimize this function over all chords to find the narrowest chord. You might try and find a function that has a nice maximum too – corresponding to the ‘thickest’ chord. In which case, probably the ellipse would have a minimum on the minor axis and a maximum on the major axis. Which I guess would mean that you want a function that is constant on every chord of a circle… Shouldn’t be too hard to cook one of those up.

Andrew Lobb.

2011-11-26 15:49:29

Hi Aaron – Long time no see. Nice solution.

Andrew Lobb.

2011-11-26 15:55:08

Sup. Try and generalize it to more interesting corridors eg with 7 bedrooms:

     .
     .
     .
  .     .
.         .

Well, we have a solution for that one now – but how about lengthening each of those branches by an extra bedroom?… No idea.

Matthew Taylor

2011-11-29 16:27:46

Had a few minutes spare to try this out; a graph with arbitrarily many 2-branches from a central vertex can be solved, but lengthening each of those branches by 1 more vertex has no solution.

The next step is: if we have a setup with a central vertex and arbitrarily many 2-branches, how many branches can we lengthen by one room before we get no solution? I have a hunch that we can have one 3-branch and still find a solution, but if we have two 3-branches we can’t. It’s tricky to think through in my head and I haven’t had a go at it yet.

I think the ultimate goal would be to find some property of graphs which tells us whether there is or isn’t a solution. We can probably reduce the general problem to a relatively small set of graphs because any graph with a simple cycle going through 3 vertices won’t have a solution and any graph with two edges between a pair of vertices is the same as the graph with just one edge between the same pair.

So the only solvable graphs are trees. First point of attack would probably be distance between vertices of degree != 2. I hope the Prince is a graph theorist; this could get difficult.

Robert Botcherby

2011-11-30 13:17:44

I had another think about a possible resolution of this problem too, possibly connected and also using circles. If we are only looking at plane shapes enclosed by simple closed curves then we can in some sense ‘inflate’ them until they become a circle. If we construct a ‘nice’ continuous deformation $f$ (possibly an ambient isotopy, although this is probably not strong enough) of the curve into a unit circle, then the narrowest bits are those which had to be ‘inflated’ furthest; if we take all pairs of diametrically opposite points $a$ and $- a$ then the narrowness is the smallest distance $d (f_{- 1} (a), f_{- 1} (b))$ .

David Cushing

2011-12-05 19:54:44

3 lots of 3 branches does have a solution. The way I think about them is two colouring the tree red and blue. I then assume that the princess is on one of the colours, say red, and then a solution to catch her can be found easily normally. If this solution took an even number of moves I add a dummy move to make it odd. This means that if the princess was on blue originally she is now on red. I then do my red solution again to catch her.

christianp

2011-12-05 19:55:47

Prove it! I want cold hard vertex sequences!

David Cushing

2011-12-05 20:17:50

Call the centre O the ones attached to that A,B and C and the ones next to them a,b and c. Let the centre be red and assume the princess is on red. Do aAOCOBb. If she is not caught she must of been on blue originally and now must be on red. Now do aAOCOBb again and she is caught.

Andrew Lobb.

2011-12-13 14:13:55

I think we meant that there are 3 edges in each branch, so say 10 vertices in total. I’d like to see a proof that this doesn’t have a solution.

christianp

2011-12-13 14:18:32

The proof involves exhausting all possible strategies! I took advantage of the symmetries of the graph to reduce the effort. David and I now have a proof that only trees not containing the three-spokes-of-three graph are solvable. We’re going to write it up, but we’re busy with our respective theses. I can explain it to you at MathsJam. Have you seen my interactive version of the puzzle? http://checkmyworking.com/misc/princess-castle/