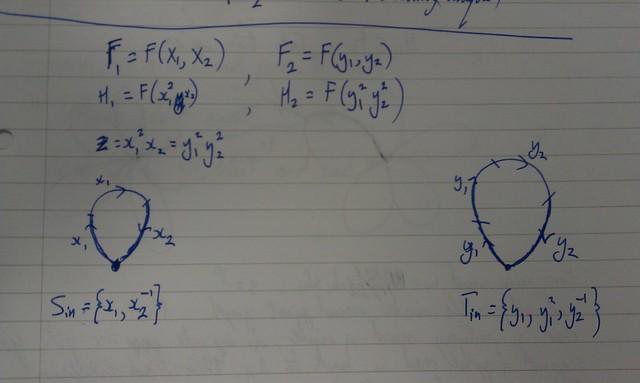Liza Frenkel is visiting the department, and she wants me to write an algorithm to compute double coset representation normal forms for free products with amalgamation.

Here are some notes I typed up in write maths, see maths as she and Andrew talked. I’m just putting them up here so I don’t lose them.

Suppose:
$F_1$, $F_2$ free groups (finitely generated by $X$ and $Y$, respectively)
$H_1\le F_1$, $H_2\le F_2$
$\mathrm{\exists }$ an isomorphism $\varphi :H_1\to H_2$
i.e. we have a finite generating set (in fact a basis) $\{h_1,\dots ,h_n\}$ for $H_1$ (and$\{h_1\prime ,\dots ,h_n^{\prime }\}$ for $H_2$) and generating sets $X,Y$ for $F_1$ and $F_2$

Consider a group generated by $z_1,\dots ,z_m$, with
$z_1=h_1(x_1,\dots ,x_n)=h_1\prime (y_1,\dots ,y_r),\dots ,z_m=h_m(x_1,\dots ,x_n)=h_m^{\prime }(y_1,\dots ,y_r)$
$G=F_1\underset{H_1=H_2}{\ast }{F}_2$ has presentation $⟨X,Y|h_i=h_i^{\prime },i=1\dots m⟩$
Choose a set $S\subseteq F$ such that $F_1={\displaystyle \bigcup _{s\in S}{H}_{1}s{H}_1}$
(we are assuming $S$ is infinite)
every element $w$ of $F_1$ is equal to $w=h_{1}s{h}_2$, for unique $s\in S$,
$h_1,h_2\in H_1$
can do the same for $F_2={\displaystyle \bigcup _{t\in T}{H}_{2}t{H}_2}$

Let $g\in G$.
A word $w$ representing $g$ is in normal form if $w=h_{i_1}(z)p_1{h}_{i_2}(z)p_2\dots h_{i_k}(z)p_k{h}_{i_{k+1}}(z)$, with $p_i\in S$, $i=1\dots k$.

Suppose $g=g_1{g}_2\dots g_k$. Rewrite using double coset representatives
$g=h_1(X)s_1{h}_2(Y)t_2{h}_3(X)\dots$

$g$ is in reduced form if $g=g_1\dots g_k$ and
$k=1\Rightarrow$ $g\in F_1$ or $g\in F_2$
$k>1\Rightarrow g_i\in F_1\mathrm{\setminus }{H}_1$ or $g_i\in F_2\mathrm{\setminus }{H}_2$ and $g_i$, $g_{i+1}$ belong to different factors

Let ${\mathrm{\Gamma }}_{H_1}$ be a folded subgroup graph of $H_1$. Take two copies.

For some word $w=h_{1}s{h}_2$, the question is how to find $s$.

Algorithm:
Read all possible loops round first graph, to get $h_1$.
Keep reading letters round the graph until there is no edge corresponding to the current letter. Call this $s_1$.
Start at the other end, reading loops to get $h_2$, and then maximal $s_2$ partway round a loop.
Then either there are no letters left to look at, and $s=s_1{s}_2$, or some bit $f_0$ in the middle, and $s=s_1{f}_0{s}_2$.

We want $h_1,h_2,s$ to all have maximal length.

Example

i) $\begin{array}{rl}g& =x_1^3{x}_2^2{y}_1{y}_2\\ & =(x_1^2)(x_1{x}_2)(x_2^{-1}{)}^{-1}\cdot (y_1)(y_2^{-1}{)}^{-1}\end{array}$

Membership problem

$$\begin{array}{rl}G& =F_1\underset{H_1=H_2}{\ast }{F}_2\\ H_3& =⟨c_1,\dots ,c_l⟩⩽G\end{array}$$
Can write the $c_i$ in normal form.
Question: Given $w\in G$ in normal form, is $w\in H_3$?

Constructing a folded graph which makes use of the normal form is tricky.

Over Christmas I typed up my Bass-Serre / Grzegorczyk stuff in quite a lot of detail and fairly rigorously. It’s far too much to put up here as blog posts, so here’s a link to the PDF.

The big theorem I prove says that the fundamental group of a graph of $E_n$-computable groups is $E_{n+1}$-computable. But are there cases when the fgoagog stays at $E_n$, and can we pin down what conditions cause it to move up to $E_{n+1}$? I’ve found a couple of examples which begin to answer those questions.

Corollary 1 says that if the edge groups are finitely generated then you don’t go up a level, while Corollary 2 gives an example of a graph with infinitely generated edge groups that does go up a level.

Little Facts

1. The $n$^th prime $p_n\approx n\log n$.
2. $\exp (x,y):=x^y\in E_3$.
3. The Gödel encoding of a word of length $n$ on an alphabet $X$ is $\le p_n^{J(n,n)}$, an $E_3$ function.

Theorem 6.7 (from the paper)

Suppose we have $G={\pi }_1(\mathbf{G},\mathrm{\Gamma },T,v_0)$, where $\mathrm{\Gamma }$ is finite. Suppose all the $G_i\in \mathbf{G}$ are finitely generated $E_n$-computable groups, $n\ge 3$. Assume all the identified subgroups are $E_n$-decidable, and all the isomorphisms ${\varphi }_e$ are $E_n$-computable. Then $G$ is $E_{n+1}$-computable.

Corollary 1

Same assumptions as the Theorem 6.7, but also assume that the edge groups are finitely generated. So each edge homomorphism ${\varphi }_{e_{ij}}$ sends a finitely generated subgroup $E_{ij}\le G_i$ to another finitely generated subgroup $E_{ji}\le G_j$. Suppose everything is $E_n$-computable.

Then $G={\pi }_1(\mathbf{G},\mathrm{\Gamma },T,v_0)$ is $E_n$-computable.

Proof

In the algorithm from Theorem 6.7, the potential for unbounded recursion comes from applying the edge homomorphisms repeatedly. We will show that the result of applying the edge homomorphisms repeatedly is bounded by an $E_3$ function.

Let $w$ be a word on $G$ of length $n$. An upper bound on the number of syllables in $w$ is $n$, so let’s say there are $n$ applications of edge homomorphisms.

A homomorphism ${\varphi }_{e_{ij}}$ rewrites generators $x\in X_i$ as words ${\varphi }_{e_{ij}}(x)\in X_j^{\ast }$. As $G-i$ is finitely generated, there is a word ${\varphi }_{e_{ij}}(x)$ of maximum, finite length $k_{ij}$. So a word $w_i\in E_{ij}$ of length $m$ is rewritten to a word $w_j\in E_j$ of length at most $k_{ij}m$.

Because the graph is finite, we can find a greatest $k\in \{k_{ij}\}$. So after reducing all the syllables (assuming that can be done for the input word), the resulting word in $G_0$ has length at most $k^{n}n=L$.

Hence the index of the resulting word is bounded by

$$p_{k^{n}n}^{J(k^{n}n,k^{n}n)},$$

an $E_3$ function, by Fact 2. So recursion on the edge homomorphisms is bounded by an $E_n$ function, and so $G$ is $E_n$-computable.

$◻$

Corollary 2

We will construct a graph of $E_3$-computable groups whose fundamental group is $E_4$-computable.

Let $\mathbf{G}=\{G_0,G_1\}$ be two copies of the free group on two generators, so $G_0=⟨x,y⟩$ and $G_1=⟨a,b⟩$. The graph has a single edge $e$ from $v_0$ to $v_1$, so $\mathrm{\Gamma }=T=(\{v_0,v_1\},\{e,\overline{e}\})$.

Let $E_{01}=⟨\{x^{-n}y{x}^n,n\in \mathbb{N}\}⟩$, $E_{10}=⟨\{a^{-n}b{a}^n,n\in \mathbb{N}\}⟩$. So the edge groups are infinitely generated.

Define

$$\begin{array}{rl}{\varphi }_e(x^{-2n}y{x}^{2n})& =a^{(-2n)!}b{a}^{(2n)!},\\ \\ {\varphi }_{\overline{e}}(a^{-2n-1}b{a}^{2n+1})& =x^{-(2n)!-1}y{x}^{(2n)!+1}.\end{array}$$

Then $G={\pi }_1(\mathbf{G},\mathrm{\Gamma },T,v_0)$ is $E_4$-computable.

Proof

First of all, the homomorphisms are $E_3$-computable because words of the form $a^{-n}b{a}^n$ can be recognised by an $E_3$ function. Hence all the ingredients of the graph of groups are $E_3$-computable.

A word of the form

$$e{a}^{-1}{e}^{-1}\dots x^{-1}e{a}^{-1}{e}^{-1}{x}^{-n}y{x}^{n}ea{e}^{-1}x\dots ea{e}^{-1}$$

will be reduced to a word on $G_0$ whose length is proportional to ${\mathrm{fact}}^{(m)}(n)$, where $m$ is the number of syllables. As $m$ depends on the input, this length can only be computed by unbounded recursion on an $E_3$ function, so is only $E_4$-computable.

Therefore, $G$ is $E_4$-computable. $◻$

In order to define a free product with amalgamation $A{\ast }_{C}B$ you need to define $A,B,C$ and embeddings of $C$ into $A$ and $B$. Alternatively, instead of $C$ you can use a homomorphism $phi:A\to B$ and its inverse. A third option is to pick subgroups $D\subset A$ and $E\subset B$ and give an isomorphism between them.

All three of these options require you to define some groups and some morphisms. You can define a group nicely by giving a presentation but defining maps usually takes a few lines. So, I’d like a quicker way of describing the kinds of maps we need here.

Let’s take the third option. If we have generating sets so that $D=⟨X⟩$ and $E=⟨Y⟩$, then if we can write each of the elements of $X$ as words in $Y^{\ast }$ then that defines the required isomorphism completely. After you’ve done that, the generating set $Y$ might as well just be those words.

So how about this as a presentation for an FPA?

$$⟨a_1,a_2,\dots |R_A⟩[x_1=y_1,x_2=y_2,\dots ]⟨b_1,b_2,\dots |R_B⟩$$

The bits in angle brackets are presentations of $A$ and $B$. The $x_i$ are words from $A$ and generate $D$, and the $y_i$ are words from $B$ and generate $E$.

Because this is all on one line and delimited adequately, you can chain things together and use brackets and all that, like this contrived example:

$$(⟨a,b⟩[b=c]⟨c,d|cd=dc⟩)[a=e]⟨e,f⟩$$

For HNN extensions, you just need to say what the original group is, what the extending letter is, and what the identified subgroups are. So how about something like:

$$⟨g_1,g_2,\dots |R_G⟩[t|x_1=y_1,x_2=y_2,\dots ]$$

Apart from the different kinds of brackets being hard to distinguish visually, what have I missed?

I’m going to write up a result I think I’ve proved, which follows on from Gatterdam’s thesis. He showed that if a group is $E_n$ computable, then doing a free product with amalgamation or any number of HNN extensions to it results in a group which is at worst $E_{n+1}$ computable. What I’m going to say is that the fundamental group of a graph of $E_n$ groups is at most $E_{n+1}$ computable. This isn’t unreasonable, because a fgoagog (( ‘fgoagog’ is short for ‘fundamental group of a graph of groups’, because I can’t be doing with writing that out once every three minutes )) represents a load of HNN extensions and amalgamated products.

The tactic will be to follow Gatterdam’s method for amalgamated products – if we can find an algorithm which solves the word problem of the fgoagog (decides if a word on the generators is equivalent to the identity) in $E_{n+1}$ time, then the whole group is $E_{n+1}$ computable as a quotient of the free group by the set of trivial words.

I will define an admissible form for words from the fgoagog, which is an alternating series of edge letters and words from the vertex groups, such that the edge letters make up a cycle starting and ending at the base vertex. Once we have a word in admissible form, we can reduce it by swapping the image of an edge group in one vertex with its counterpart in the vertex at the other end, and eventually a trivial word will end up as just a word on the base vertex, which is an $E_n$ decision.

Clearly the process of putting a word in admissible form involves knowing something about the shape of the graph, so we need to make some $E_n$ computable functions which can represent the graph and compute paths between vertices. That’s a tiny bit interesting on its own, so I’ll spend my next post talking about that. It will need some pretty pictures of trees though, which is why I’ve put off writing it for so long.