Zero-knowledge protocols

by cp!

Zero-knowledge proof

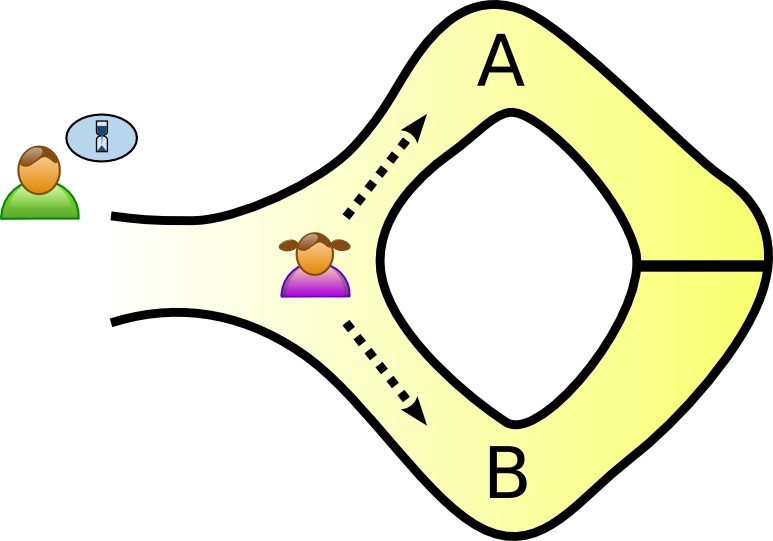
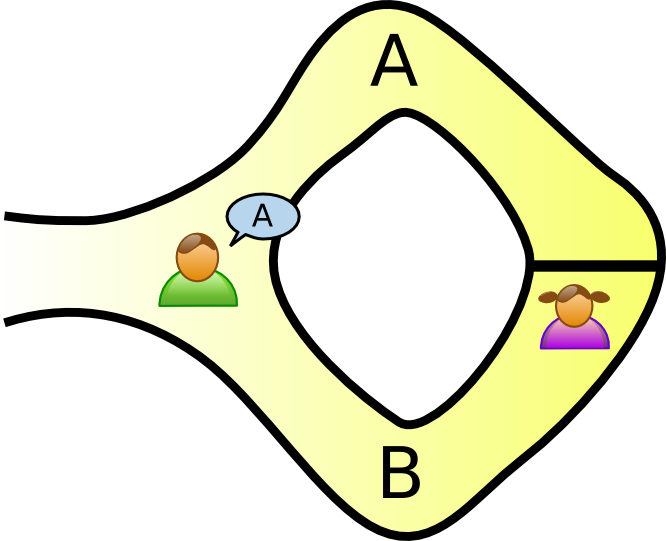
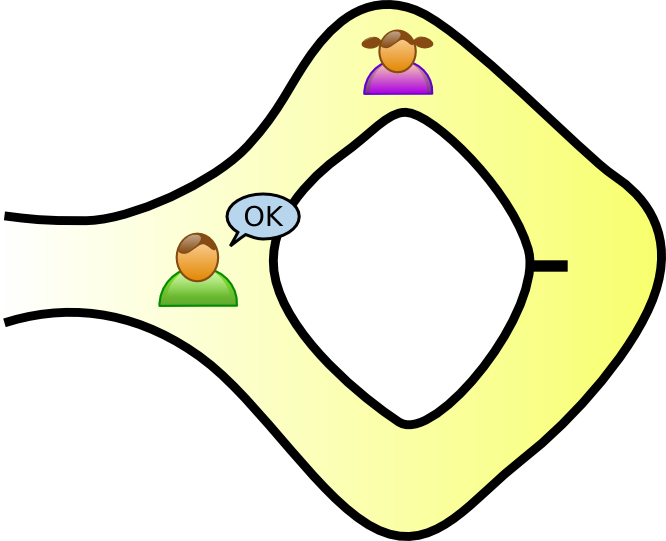
A zero-knowledge proof is an interactive method for one party to prove to another that a statement is true without revealing anything other than the veracity of the statement.

Definition

(from A Survey of Zero-Knowledge Proofs with Applications to Cryptography, A. Mohr.)

An interactive proof system is a two-party game between a verifier executing a probabilistic polynomial-time strategy and a prover which executes a computationally unbounded strategy satisfying:

An interactive proof system is zero-knowledge if the output of any strategy used by a cheating verifier could also be produced by a non-interactive computation alone.

That is, even if the verifier is trying to cheat, they learn nothing other than whether the statement is true, unless they were already able to verify the statement independently.

A really simple example

from How to Explain Zero-Knowledge Protocols to Your Children, Quisquater, Jean-Jacques; Guillou, Louis C.; Berson, Thomas A. (1990).

Some more serious applications

Graph isomorphism

(from Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems, O. Goldreich, S. Micali, A. Wigderson, 1991.)

Graphs $G(V,E)$ and $H(V,F)$ are isomorphic iff there exists a permutation $\pi$ of the set of vertices $V$ such that \[(u,v) \in E \: \Leftrightarrow \: (\pi(u),\pi(v)) \in F\].

Protocol

We have two graphs $G_0(V,E_0)$ and $G_1(V,E_1)$. V wants P to prove that they are isomorphic. Let $G_1 = \phi G_0$.

  • P generates a random isomorphic copy $H$ of $G_1$, by selecting a permutation $\pi \in S_{|V|}$. P sends $H$ to V.
  • V chooses $\alpha \in \{0,1\}$ at random and sends it to P, i.e. "Are $H$ and $G_{\alpha}$ isomorphic?".
  • If $\alpha = 1$, P sends $\pi$ to V, otherwise P sends $\pi \cdot \phi$.
  • If the permutation $\psi$ received by V is not an isomorphism between $G_{\alpha}$ and $H$, then the verifier stops and rejects.

After $m$ successful iterations of these steps, V accepts P's proof.

Some more serious applications

NP problems

If we can construct a zero-knowledge protocol for any NP-complete problem, it can serve as a zero-knowledge protocol for any NP problem. So, pick one!

Graph three-colourability

I have a graph $G(V,E)$. Can its vertices be coloured with exactly three colours so that no edge has the same colour on both ends?

Protocol

Both P and V know a graph $G(V,E)$ with $|V| = n, |E| = m$. P claims to know a 3-colouring $\phi:V \rightarrow \{1,2,3\}$ of G. Do the following $m^2$ times:

  • P chooses a random permutation $\pi$ of $\{1,2,3\}$ and composes it with $\phi$. For each vertex $v$, P places $\pi \cdot \phi(v)$ in a locked box labelled $v$. P then sends the locked boxes to V.
  • V asks P about a randomly chosen edge $e = (u,v)$.
  • P sends V the keys to boxes $u$ and $v$.
  • If the keys don't match the boxes, or the colours inside the unlocked boxes are the same, V rejects the proof.

Poker

How do you play Poker over the internet without a trusted dealer? This is called mental poker.

We need to ensure the following:

The paper, A zero-knowledge Poker protocol that achieves confidentiality of the players’ strategy or How to achieve an electronic Poker face, C. Crépeau (1987), gives a zero-knowledge protocol satisfying all these requirements.

Basic outline of the protocol

Every player $P_i$ secretly picks a shuffling of the cards $\pi_i$. The shuffled deck is $\pi = \pi_N \dots \pi_2 \pi_1$.

To pick a card, select a number $k \in \{1,\dots,52\}$ which hasn't been picked yet, and compute $\pi(k)$.

Computing $\pi(k)$ so that only the player taking the card knows its value involves lots and lots of zero-knowledge protocols.

Sudoku!

Somebody is going to prove that they can solve my Sudoku puzzle without revealing their solution.

We'll use the protocol from Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles, Gradwohl, R., Naor, M., Pinkas, B., & Rothblum, G. (2007).

Protocol

← →

/

#