Newcastle MathsJam January 2012 Recap

2012-02-03

January’s MathsJam was a bit massive. It’s now a week later and I’ve only just gathered enough thoughts together to do this writeup.

There were nine of us this month, all but one of whom either maths students or lecturers. A major theme of the night was of professional mathematicians or nearly-professional mathematicians forgetting basic high-school methods. This led to quite an intense session of puzzling and proving.

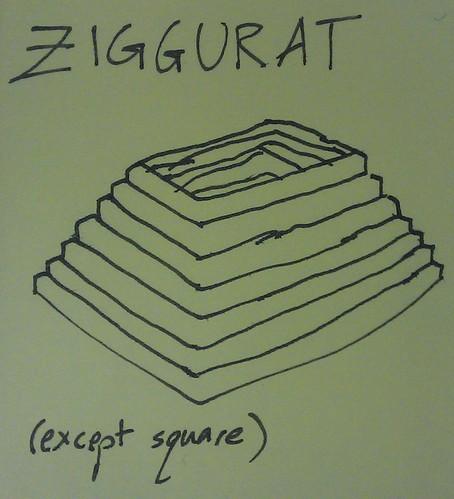
Things didn’t start out that way, though. A few weeks ago I found the website of a mathematician in Illinois called Alan Schoen, and his page about Lominoes. They’re a pretty interesting set of shapes! I ordered a couple of sets and they arrived just in time for the MathsJam.

We spent a lot of time trying to build a ziggurat:

Because I had two sets, we split into two teams and the competition got a bit serious. The spirit of friendly cooperation was away on a business trip.

Team A (best team, my team) did a lot of writing and calculations and thinking. We hardly touched a piece other than to measure it.

Team B, on the other hand, were much more hands-on in their deliberations. They got quite emotionally involved with the pieces – when I asked why a particular pile of pieces wasn’t being touched, I was informed that those were the “bad” pieces.

A key point of contention was the question of which pieces needed to be used. I think we settled on everything except the greys and half the blues.

We spent well over an hour trying to build a ziggurat. Neither team succeeded: both teams failed. While packing the pieces away, Andrew (Team B, free spirit) constructed this challenging artwork:

Matthew Taylor again posted a puzzle on Twitter before the MathsJam night. This time it was a question about points with integer coordinates on the boundary simplex-ish shapes. We didn’t find a solution.

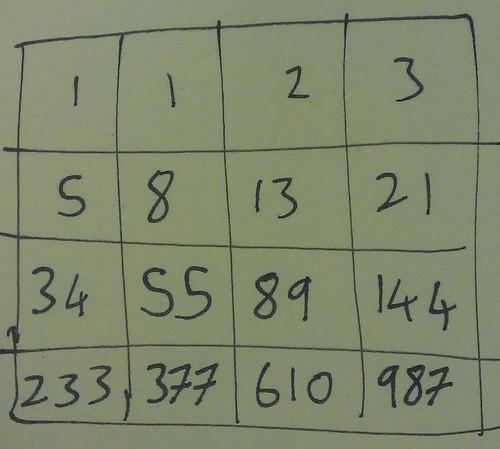
A Fibonacci fact

David Cushing showed me this fact. It’s pretty cool!

Draw an $N \times N$ grid and fill it with the Fibonacci numbers:

Pick any $2 \times 2$ square, and work out its determinant. For example,

$89 \times 8 - 55 \times 13 = - 3.$

What’s the pattern?

The others at MathsJam spotted what was going on with a little bit of prompting. Click here if you’d like a spoiler.

The determinant is always $\pm F_{N}$ . There’s a fairly straightforward proof by induction.

Click here if you want proof.

The recurrence relation for the Fibonacci series is that $F_{i + 1} = F_{i - 1} + F_{i} .$

The base case for the induction is the top-left square. The determinant of the top-left square is $F_{1} F_{N + 2} - F_{2} F_{N + 1} = F_{N + 2} - F_{N + 1} = F_{N} .$

Let $D_{i}$ be the determinant of the square whose top-left entry is $F_{i}$ . Then $D_{i} = F_{i} F_{i + N + 1} - F_{i + 1} F_{i + N}$ .

We want to show that if $D_{i} = \pm F_{N}$ , then $D_{i + 1} = \pm F_{N}$ too.

You can use that to rearrange the formula for $D_{i}$ :

$\begin{aligned} D_{i} & = F_{i} F_{i + N + 1} - F_{i + 1} F_{i + N} \\ = (F_{i + 2} - F_{i + 1}) F_{i + N + 1} - F_{i + 1} (F_{i + N + 2} - F_{i + N + 1}) \\ = F_{i + 2} F_{i + N + 1} - F_{i + 1} F_{i + N + 2} \\ = - (F_{i + 1} F_{i + N + 2} - F_{i + 2} F_{i + N + 1}) \\ = - D_{i + 1} . \end{aligned}$

Hence $D_{i + 1} = - D_{i}$ , so in fact I can be a bit more precise than before and say that $D_{i} = (- 1)^{i + 1} F_{N} .$

The Dorset MathsJam posted a problem to twitter:

DOR: 4 cups upside down. Turn over 3 at a time. Minimum number of moves to turn all right way up?

— Maths Jam (@MathsJam) January 24, 2012

This is pretty similar to the lights-out puzzle we discussed in December. It turns out that Stephen, one of the new attendees this month, had a much better proof that not all patterns in the lights-out puzzle could be produced: all of the moves change either zero or two corner squares, so patterns with an odd number of corners lit up can’t be produced.

A bug on a boinger

Andrew posed this conundrum:

I have a $1$ metre elastic band tied to my waist. I tie the other end to a wall and start walking away at $1$ metre per second. There’s a bug on the wall which decides to walk along the elastic band, at $10$ centimetres per second. Does it ever reach me?

After you’ve had a think, click here for the answer.

We solved this basically by writing down everything we knew.

Call the distance of the bug from the wall $x (t)$ and the distance of the end of the elastic band from the wall $l (t)$ .

$l (t)$ increases by $1$ metre per second, so write that down as a differential equation:

$\frac{d l}{d t} = 1.$

In fact, we can just write down $l (t)$ , assuming that the band is taut at $t = 0$ :

$l (t) = t + 1.$

The bug walks at $10$ centimetres per second, or $\frac{1}{10}$ metres per second. But the band is also stretching, which propels the bug forwards a bit. Assuming the band stretches uniformly, the point that the bug is standing on moves forwards proportional to the fraction of the band that is behind it, i.e. $\frac{x}{l}$ .

We can then write down a differential equation for the bug’s position:

$\begin{aligned} \frac{d x}{d t} & = \frac{1}{10} + \frac{x (t)}{l (t)} \\ = \frac{1}{10} + \frac{x}{t + 1} . \end{aligned}$

I think we were all a bit tired at this point from trying to make the Lominoes to fit together, so we were staring at that equation for a good while, despairing that we couldn’t remember the method for solving it.

Luckily, Ji was a little bit more awake than the rest of us and applied the integrating factor method.

$\begin{aligned} x (t) & = \frac{1}{10} (t + 1) \ln (t + 1) \\ = l (t) (\frac{1}{10} \ln (t + 1)) \end{aligned}$

So, since the bug is eventually moving faster than I am, it does reach the end of the elastic band.

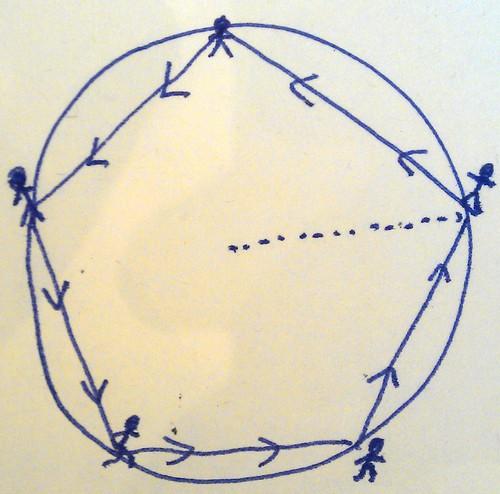
Emboldened by his solution to the last puzzle, Ji posed this question

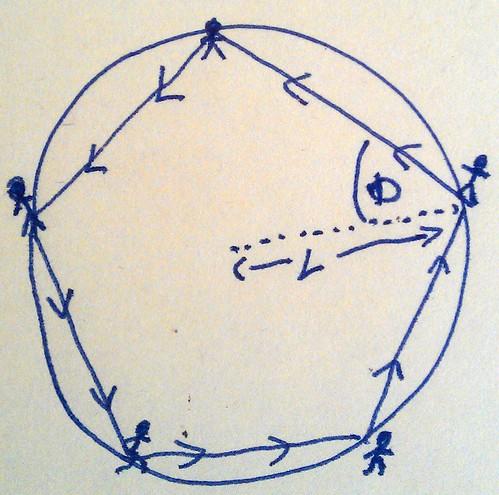
Silly people chasing each other

There are $5$ people spaced evenly around a circle. Each person is chasing the person to their right, taking the shortest route instead of walking around the edge of the circle. They’re all moving at the same speed. What happens?

Working out what happens shouldn’t take too long. Working out when it happens involves a bit of geometry. If you’d like to see the answer, click here.

Since each person is running into the circle, they eventually all collide in the middle. They’re all running at the same speed and angle from the tangent, so the regular pentagonal arrangement is preserved and each person’s path is a spiral. That means that we only need to think about how quickly each person is moving towards the centre, and we can forget about the rotation.

It doesn’t really matter how fast the people are running in absolute terms, just how fast they’re running in proportion to the size of the circle. So say that the people are running at $1$ unit per second, and the circle has a radius of $L$ units.

Now, since the people are always on the points of a pentagon, the angles between them are always the same. For any person, call the angle between the middle of the circle and the person they’re chasing $θ$ .

The part of the person’s velocity which is moving inwards is $\cos θ$ . This doesn’t depend on the time! So, although the people will be turning faster and faster, they will always be moving inwards at the same rate.

That means that the silly people will reach the middle of the circle and either bump into each other or achieve the dizziness singularity after $\frac{L}{\cos θ}$ seconds.

You’ll notice I didn’t bother working out what $θ$ is. It’s just half the interior of the angle of the polygon. Ji posed the puzzle with five people originally, but there’s no reason not to work it out for a general number $N$ . According to GCSE Bitesize, the interior angle of an $n$ -gon is $180 (1 - \frac{2}{n}) .$

With that in mind, here’s a formula for the time of collision in terms of $N$ :

$t_{k e r p l o w!} = \frac{L}{\cos (90 (1 - \frac{2}{n}))}$

Andrew had another puzzle. It had more of us stumped than the England cricket team in their recent test matches.

The worst sequence in the world

$\dots, 7, 9, 12, ? ?, 24, 36, 56, 90, \dots$

Andrew quite rightly tried to avoid giving us many hints about this. When I got it, I felt like slapping him in the face. You need to experience this feeling too.

Click here for the first hint.

Try dividing every number by $24$ .

Spend a while thinking about that. If you’re really stuck, click here for the second hint Andrew gave.

After dividing by $24$ , the numbers look like this if you write them down as reduced fractions.

$\dots, \frac{7}{24}, \frac{3}{12}, \frac{1}{2}, ? ?, \frac{1}{1}, \frac{3}{2}, \frac{7}{3}, \frac{15}{4}, \dots$

Look at the numbers to the right of the unknown entry.

Take a good long hard look. This is where I realised what was going on. If you’re defeated, click here for the solution.

The terms of the sequence are $24 \cdot \frac{2^{n} - 1}{n} .$

The problem is, the unknown term corresponds to $n = 0.$ So what is the value of $\frac{2^{0} - 1}{0}$ ? It looks like it should be $\frac{0}{0}$ .

Fortunately, one of the Durham undergrads was cleverer than me. What we really want is

$lim_{n \to 0} (24 \cdot \frac{2^{n} - 1}{n})$

I was informed that the value of that limit is $24 \ln 2$ . I don’t know why that is the value. My brain needed rest.

There was a brief break from puzzling when I told everyone that I was taking notes for a Mathematics Today article, and I wanted to hear how everyone was feeling.

Several of the undergrads said that they’d spent four years studying maths and thinking they were pretty good, until they came to MathsJam and had a go at some of the puzzles. They were happy about that fact. I think Andrew and I do give them some very hard puzzles precisely because they’re keen undergrads, though.

We were all agreed that MathsJam keeps you on your toes – “Why don’t I know this? It’s first year stuff!” was a common exclamation throughout the evening.

Matthew asked a couple of questions about PhD interviews – in particular, how formal they are. Answer: not very. They’re mainly for you and your supervisor to see how well you’ll get along.

This led to a discussion of tropical maths because Matthew had visited a potential supervisor about a project in that field.

Tropical maths

In tropical maths, the addition and multiplication operations are different to the usual ones. They’re called $\oplus$ and $\otimes$ and they work like so:

$\begin{aligned} x \oplus y & = min (x, y) \\ x \otimes y & = x + y \end{aligned}$

So $3 \oplus 4 = min (3, 4) = 3$ and $3 \otimes 4 = 3 + 4 = 7$ .

Apparently you can solve sets of simultaneous equations with these operations. I just made one up, and it works:

$\begin{aligned} x \oplus 2 y & = 1 \\ 3 x \oplus y & = 2. \end{aligned}$

In the usual arithmetic, that means:

$\begin{aligned} min (x, y + 2) & = 1 \\ min (x + 3, y) & = 2. \end{aligned}$

But I’ll stick with the tropical notation. My first thought is to multiply the first equation by $3$ so that the coefficients of $x$ are the same in both equations:

$\begin{aligned} (3 \otimes x) \oplus (3 \otimes 2 \otimes y) & = 3 \otimes 1 \Leftrightarrow \\ 3 x \oplus ((3 + 2) y) & = 3 + 1 \Leftrightarrow \\ 3 x \oplus 5 y & = 4 \end{aligned}$

So the simultaneous equations now look like this:

$\begin{aligned} 3 x \oplus 5 y & = 4 \\ 3 x \oplus y & = 2 \end{aligned}$

or,

$\begin{aligned} min (x + 3, y + 5) & = 4 \\ min (x + 3, y) & = 2 \end{aligned}$

It follows that $x + 3 = 4$ , so $x = 1$ , and $y = 2$ . How interesting! Abstract algebra is the best.

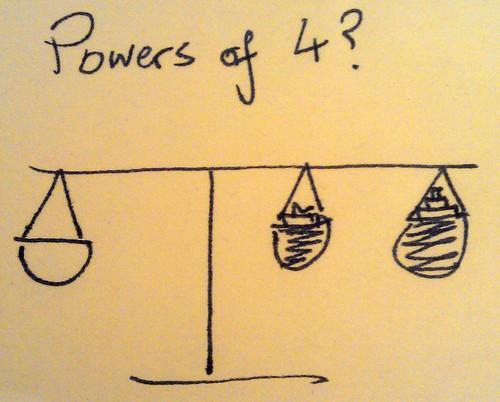
There was some talk about Golomb rulers, which have the property that any length can only be measured at most one way. A similar question is the smallest set of weights you need to be able to measure any whole number of units on a set of scales – it’s powers of $2$ if you can only put weights on one side, and powers of $3$ if you can put weights on either side. We wondered what setup would use powers of $4$ .

Ji kept trying to get me to think about how to fit $72$ T-shaped tetrominoes (tetrominoids?) together into a $6 \times 6 \times 6$ cube. I had no idea where to begin. Hopefully in February he’ll bring some along and explain what he was on about.

Andrew mentioned a question that the London MathsJam had apparently discussed in November and December but not found a satisfactory answer to.

Maximising your profit from an awkward benefactor

Somebody presents you with two envelopes containing money. One envelope contains twice as much money as the other. You’re asked to pick one envelope. It turns out that the envelope you pick contains £10. You’re offered the chance to switch to the other envelope. Should you?

Andrew and I were fairly satisfied with our answer, but the others either weren’t convinced or had come to different conclusions. I’ll let you discuss this in the comments thread. It’s a rather finicky question.

As we were just about to get ready to leave, I mentioned that while writing an edition of the Internet Maths Aperiodical I had found out that there are $85$ ways to tie a tie, $43, 200$ ways to do up your shoelaces and (at least) 25 ways to wear a scarf.

So the question naturally arose:

How many ways are there for a banker to dress himself?

We came up with a fairly extensive list of configurably-worn items:

Tie
Shoelaces $\times 2$
Scarf
Shirt – buttons done/undone, map buttons $\to$ buttonholes, inside-in or inside-out, sleeves rolled up or not, etc.
Placement of phone, wallet, keys in pockets
Order of notes and cards in wallet

We thought this provided enough combinations to allow every banker who has ever lived to dress uniquely. So why are they not‽

Finally, someone asked if David and I had made any more progress on the dragon-catapult puzzle mentioned last month. I regretted to inform them that we’ve decided it’s unsolvable in too many cases to be interesting. Someone, possibly Tash, asked what would happen if, instead of firing a catapult at the dragon, we had to chase it on foot. This is an old problem, most often stated in terms of lions trying to catch gladiators.

Very finally, Matthew asked if you can prove anything non-trivial in a tweet. The next day, he tweeted this:

Infinitely many primes: assume there aren’t, take the product of them all, add one, decompose, get a new prime. #twitterproof #MathsJam

— Matthew Taylor (@AdrenalGBR) January 25, 2012

And that was the end of January’s MathsJam! It was a marathon. I was intellectually exhausted for days afterwards. I’m going to try to take some games to play next month, so we don’t do quite so many difficult puzzles. We need more amateur mathematicians, too!

Comments

David Cushing

2012-02-03 23:26:35

Very good write up as usual

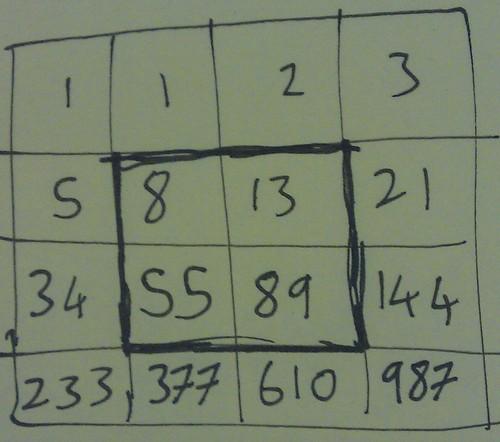
A couple of comments about the Fibonacci grids. You can also try it with drawing any sized square inside the grid and looking at the determinant of the corners.

I’m also interested in putting arbitrary sequences in an NxN grid. My main question is for what sequences can we put inside a NxN grid such that the possible values of the 2×2 determinants can only have a finite number of values as N tends to infinity. We have seen that the Fibonacci numbers there are two possible values. For linear sequences there is 1 possible value

Chris M. Dickson

2012-02-21 23:47:51

Thanks, the February MathsJam was fun!

By any chance, did a small piece of orange translucent plastic turn up at all? 66 octiamonds went out and only 65 came back. My fault totally for getting them out too late, not putting them away early enough and/or sweeping them all onto the floor instead of into my bag, and/or for parking in a garage which claimed to close at 10 o’clock. This does seem like a long shot but you never know!

Christian Perfect

2012-02-22 11:29:20

Oh dear! I feel really bad because that was a serious set of octiamonds. I tweeted last night to ask if anyone had it but I haven’t had any replies.

Chris M. Dickson

2012-02-23 20:31:53

Thank you; I appreciate it. I’m hopeful that it’ll turn up in the car, having fallen out on the seat, or similar.