This post is about the best logic puzzle I’ve seen in absolutely ages. It’s easy to explain and doesn’t require any silly tricks, but has a decent amount of depth to it and challenges your intuition. I’m going to present the puzzle, an extended version of the puzzle, and a general solution to the extended version.

The “classic” puzzle was told to me by David Cushing, who was told it by Alistair Bird, who himself found it on the MathOverflow “math puzzles for dinner” thread.

The setup goes like this:

• there is a castle with 17 rooms in it, arranged in a line.
• the princess who lives in the castle sleeps in a different room each night, but always one adjacent to the one she slept in the previous night. She is free pick any room to sleep in on the first night.
• a prince would like to find the princess, but she will not tell him where she is going to sleep each night.
• the prince can look in a single room each night, with no other restrictions

And the puzzle is:

Is there a strategy the prince can follow to guarantee he looks in the room the princess is sleeping in within a finite number of days?

If you haven’t seen this puzzle before, look away from the screen now and spend some time working out the solution. Try starting with castles of just a few rooms, and see if you can spot a pattern in the winning strategies. This version of the puzzle is definitely solvable by just sitting and thinking for a while.

I’ve created an interactive version of the puzzle to help with trying out strategies. The interactive version keeps track of where the princess can be at any point in time. Can you spot a pattern in the set of rooms the Princess can be in at each stage of the strategy?

If you have seen this puzzle before, or if you’ve given up (don’t give up! Have another go, then come back here. Finding the correct solution is much more satisfying when you’ve tried lots of other ways), here are the winning strategies for several different numbers of rooms, for reference. I’ve put links to the relevant layout in the interactive puzzle at the bottom of each solution.

4 rooms in a line.

The prince should pick $(2,3,3,2)$.

Click here to try the interactive version.

$5$ rooms in a line.

The prince should pick $(2,3,4,4,3,2)$.

Click here to try the interactive version.

17 rooms in a line

The prince should pick $(2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2)$.

Click here to try the interactive version.

These aren’t the only solutions to the puzzle. Are they the shortest? Why?

General solution

For a castle with $N$ rooms in a line, start at room $2$ and work your way along to room $N–1$, then do the same thing backwards.

Andrew Lobb came up with a very good explanation of why this works:

As a first go at a strategy, pick the rooms $(1,2,\dots ,N)$ and then $(N,N-1,\dots ,1)$. If you don’t find the princess on the first night, she must be on your right. As you move along the castle, you will either find the princess or she will swap places with you (since you’re both moving only one room at a time). On the night you pick room $N$, the princess must be on your left if you haven’t found her.

Think about the rooms as either even or odd. The princess must move from an even room to an odd room, or from an odd room to an even room, each night. So if the princess swapped places with you at some point, she must have started with the opposite kind of room to you. So staying in room $N$ two nights in a row puts you in the same kind of room as the princess, and when you walk back through the castle you will be guaranteed to find the princess.

My solution doesn’t bother with $1$ and $N$ because room $1$ is never on your right, and room $N$ is never on your left. Play with the interactive puzzle to convince yourself that this works.

Princess on a graph

So that’s the classic puzzle solved. David thought he would like more to do, so he asked: what if the rooms are laid out in any arrangement, not necessarily a line?

That is, if the layout is an arbitrary graph, can you still find a winning strategy? What does it look like?

That’s a very good question! The general solution we had for straight lines doesn’t work because it needs a path straight through all the vertices, which you can’t make in general.

Simple graphs

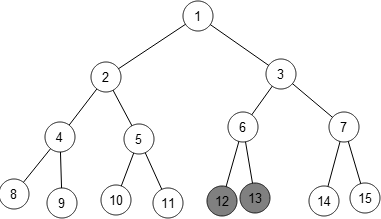
The first thing we did was to play with some simple examples to get an idea for how the puzzle works. First, we tried a binary tree with three levels. That’s solvable: one solution is $(2,1,3,3,1,2).$

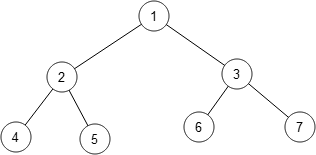
What about a triangle? It isn’t solvable – no matter what you do, the princess always has two rooms to choose from.

We were fairly sure that all binary trees could be solved. Certainly, $(4,2,5,2,1,3,6,3,7,7,3,6,3,1,2,5,2,4)$ is a solution to the binary tree with four levels, and we assumed a similar sort of strategy would work for bigger trees.

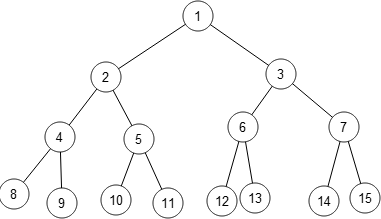
David came up with a couple of conjectures:

• if a graph $G$ contains an unsolvable subgraph, $G$ is unsolvable.
• every tree is solvable.

Only one of those is true!

MathsJam

This was as far as we got before I brought the puzzle up at MathsJam in November.

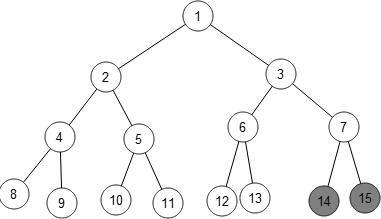
Matthew Taylor, a student at Durham, started looking at graphs with linear spokes coming out a central vertex. The first two of these are fairly easy to solve: the one with three spokes of length 1 has solution $(1,1)$, and the one with three spokes of length 2 has solution $(3,1,2,1,4,4,1,2,1,3)$.

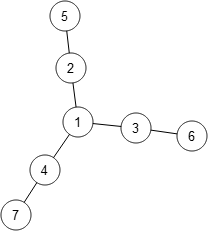
In the blog, Matthew claimed that any graph consisting of a central vertex with spokes of length $2$ coming out of it was solvable, but the same thing with spokes of length $3$ had no solution. He didn’t offer proof, but he probably had it right.

Interestingly, the graph made by extending only two spokes to length $3$ is solvable, with the strategy $(6,3,1,2,1,4,7,7,4,1,2,1,3,6)$. David calls this graph “Mario”.

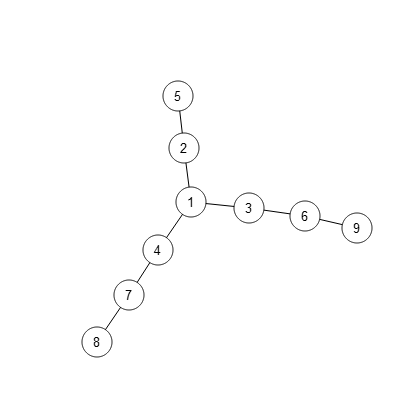
So Matthew asked, can we find a property of graphs which tells us whether there is or is not a solution? This was the insight that set us on the way to a solution.

The solution!

I’ll stop the rambling narrative now and deal out some straightforward maths. I’ll define my terms, give an algorithm which finds the shortest winning strategy for a graph, if one exists, then I’ll tell you which graphs are solvable.

Definitions

Let $G$ be the (finite) graph corresponding to the layout of the castle. Give every vertex a unique label.

The prince’s strategy is a sequence $V_1,V_2,\dots$ of labels of vertices. On night $i$, the prince looks in the room with label $V_i$.

Each night, before the prince makes his move, we can consider the state of each room: could the princess currently be in that room, or not? A room is occupiable on a particular night if there is a sequence of rooms the princess can choose which puts her in that room on that night, and differs from the prince’s strategy every previous night. If there’s no such sequence, the room is unoccupiable on that night.

Mark rooms which are occupiable with a $Y$, and rooms which are not occupiable with an $N$. A state is a $\{Y,N\}$-labelling of every vertex of the graph.

Here is how the puzzle works in this language:

1. On the first night, mark all rooms with $Y$, let $i=1$, then repeat the following:
2. Mark room $V_i$ with $N$.
3. To construct the new state of the graph: for each vertex in $G$, mark it with $Y$ if there is an adjacent vertex marked $Y$ in the previous night’s state; otherwise, mark it with $N$.
4. If all vertices are now marked $N$, the princess must have been caught on this night or a previous one no matter what she did, so the strategy $V_1,\dots ,V_i$ is a winning strategy. Otherwise, if one or more rooms are marked $Y$, let $i:=i+1$ and return to step 2.

This is just a representation of the rules of the game; it does not give us a way of finding winning strategies.

An algorithm to find the shortest winning strategy (if one exists)

Notice that there are only finitely many states a given graph can be in. So finding a winning strategy consists of finding a path from the state with all $Y$s to the state with all $N$s.

Make a couple of observations:

• Any winning strategy prepended with arbitrarily many moves will still be a winning strategy. I’d like to find the shortest winning strategy.
• If I have a strategy $V_1,V_2,\dots$ and there exists a pair $(V_i,V_j),i<j,$ such that the state of the graph on night $i$ is the same as the state of the graph on night $j$, then the moves $V_i+1,\dots ,V_j$ are redundant.

But when are two states the same? If every vertex has the same $Y/N$ labelling, certainly the states are the same, but that’s not the only case. When we were just looking at simple lines of rooms, we could start our strategy at either end, so a state which is the same as another after a reflection is really the same state.

This extends to all symmetries of the graph. For example, this state

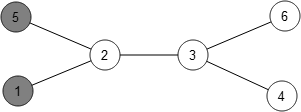
is really the same as this one

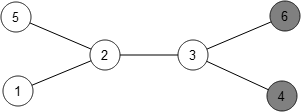
and these states are all equivalent:

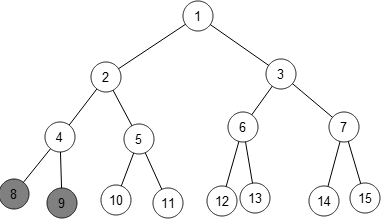
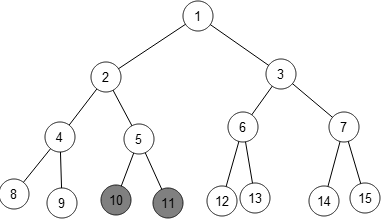
So here’s a recursive procedure for finding the shortest winning strategy for a graph:

1. The initial state has all rooms marked $Y$.
2. For each vertex $V$ marked $Y$ in the current state, compute the state the graph would be in after looking in $V$. If that state has been seen before (modulo the symmetries of the graph), then there are redundant moves in the strategy, so looking in $V$ now is not part of the shortest strategy. If the state hasn’t been seen before, perform this step on the new state.
3. Of the rooms looked at in step 2 which didn’t return null, return the room which produced the shortest strategy. If no rooms produced new states, return null.

The stuff about symmetries is just an optimisation – the above algorithm will always produce the shortest strategy even without the symmetry check, but it’s a good optimisation.

This procedure will return null iff the graph is unsolvable. But it doesn’t tell us much about which graphs are solvable.

So which graphs are solvable?

Some facts:

1. David’s first conjecture, that graphs which contain unsolvable subgraphs are themselves unsolvable is clearly true – the princess can restrict her movements to the unsolvable subgraph and there is no strategy which will find her.
2. Now note that the prince’s first move must be to look in a vertex with a neighbour of degree 1. Otherwise, every room remains occupiable on the second night.
3. So all cycles are unsolvable – they have no vertex of degree 1.
4. Facts 1 and 3 together imply that only trees can be solvable – if a graph contains a cycle, then it is unsolvable.

But which trees are solvable? David conjectured that they all are. Well, the algorithm I gave above shows that the graph with three spokes of length three joined to a central vertex (aka “threesy”) is unsolvable. Because it would take ages to describe every step, here’s a handwavey video:

So only graphs not containing “threesy” can be solvable.

What do they look like?

Let $T$ be a tree not containing threesy. We can find the longest path through $T$ and label its vertices $1,\dots ,n$. Call this path the spine. Now, every tree attached to the spine must have depth at most $2$, otherwise the spine would have to go through that tree or $T$ contains threesy. Also note that vertices $1$ and $n$ must have degree $1$.

Every such $T$ is solvable, because here’s a winning strategy:

Walk along the vertices $v_2,\dots ,v_{n-1}$, doing the following for each vertex $v_i$:

1. look in vertex $v_i$
2. for each vertex $v^{\prime }$ neighbouring $v_i$ but not in the spine, if $v^{\prime }$ has degree $>1$, look in $v^{\prime }$ and then in $v_i$ again.

Once you have finished the process for $v_{n-1}$, repeat the sequence of moves you’ve done so far, but reversed.

The reason this strategy works is the same as the reason Andrew’s strategy for straight-line castles works: on the forwards half of the strategy you are ensuring that the princess is either ahead of you or in rooms of the opposite parity to you. Once you’ve reached the end, repeating the strategy backwards puts you on the same parity as the princess, so you’re bound to find her.

So the set of solvable graphs is exactly the set of trees not containing threesy. How satisfying!

I expect to edit this post as people ask for bits to be clarified, but I really wanted to share what we’ve found, even if informally. This has been a very satisfying investigation!