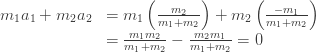Fork me on GitHub

MathJax Bookmarklet

This bookmarklet renders Tex/LaTeX, MathML and AsciiMathML notation on pages dynamically using the MathJax library.

LaTeX notation is rendered only when delimited by $, or display maths between \[ and \].

ASCIIMathML delimited by ` is rendered as well.

MathJax
Drag&Drop to your bookmarks (right-click under older IE)!

Image replacement bookmarklet

I've also made a second bookmarklet to replace the blurry image-based maths used on WordPress.com blogs and Wikipedia with nice neat MathJax. This one does all the same things as the normal MathJax bookmarklet in addition to image replacement, but I thought it would be safer to have a second bookmarklet in case it causes problems on other sites.

Use this one instead of the one above when you're on a WordPress.com blog or Wikipedia.

Replace image maths with MathJax
Replace image maths with MathJax
Drag&Drop to your bookmarks (right-click under older IE)!

Examples Execute the bookmarklet and enjoy!

LaTeX Examples

The Cauchy-Schwarz Inequality

$\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)$

Maxwell’s Equations

$\begin{aligned} \nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\ \nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\ \nabla \cdot \vec{\mathbf{B}} & = 0 \end{aligned}$

An Identity of Ramanujan

$\frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\ldots} } } }$

MathML Examples

Curl of a Vector Field

∇→×F→=(∂Fz∂y−∂Fy∂z)i+(∂Fx∂z−∂Fz∂x)j+(∂Fy∂x−∂Fx∂y)k

Definition of Christoffel Symbols

(∇XY)k=Xi(∇iY)k=Xi(∂Yk∂xi+ΓimkYm)

Standard Deviation

σ=1N∑i=1N(xi−μ)2.

AsciiMathML Example

Solving the quadratic equation. Suppose `a x^2+b x+c=0` and `a!=0`. We first divide by `\a` to get `x^2+b/a x+c/a=0`. Then we complete the square and obtain `x^2+b/a x+(b/(2a))^2-(b/(2a))^2+c/a=0`. The first three terms factor to give `(x+b/(2a))^2=(b^2)/(4a^2)-c/a`. Now we take square roots on both sides and get `x+b/(2a)=+-sqrt((b^2)/(4a^2)-c/a)`. Finally we move the `b/(2a)` to the right and simplify to get the two solutions: `x_(1,2)=(-b+-sqrt(b^2-4a c))/(2a)`

WordPress.com/Wikipedia image replacement example

(Use the WordPress.com/Wikipedia bookmarklet to replace this image with MathJax)

\begin{array}{rl} m_1a_1 + m_2a_2 &= m_1 \left( \frac{m_2}{m_1+m_2} \right) + m_2 \left( \frac{-m_1}{m_1+m_2} \right) \\ &= \frac{m_1m_2}{m_1+m_2} - \frac{m_2m_1}{m_1+m_2} = 0 \end{array}